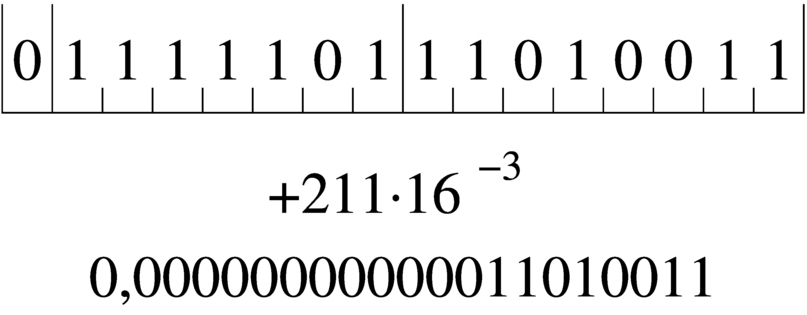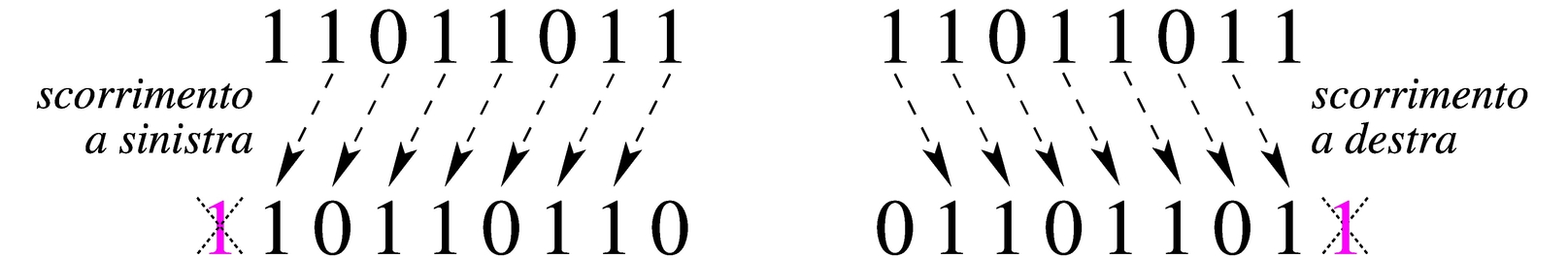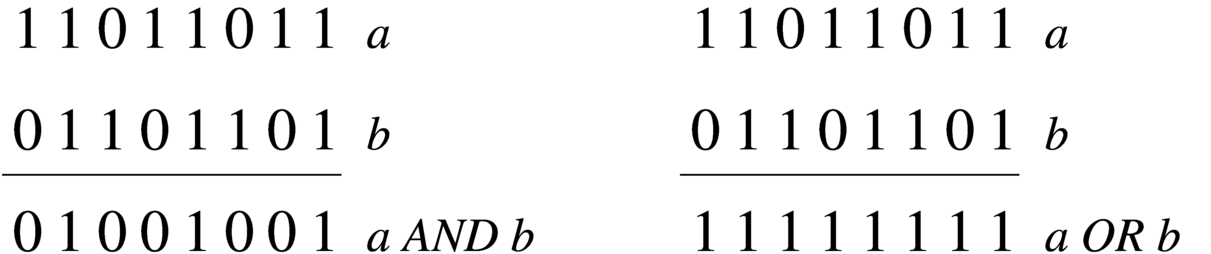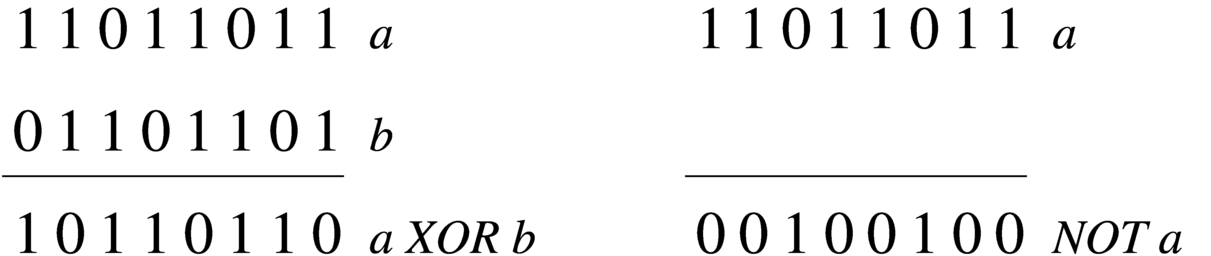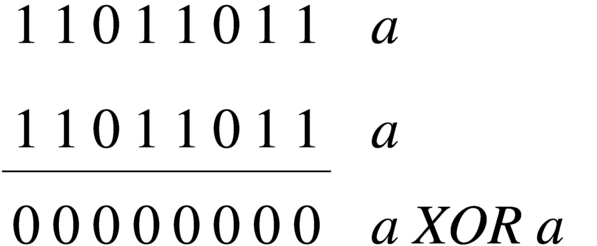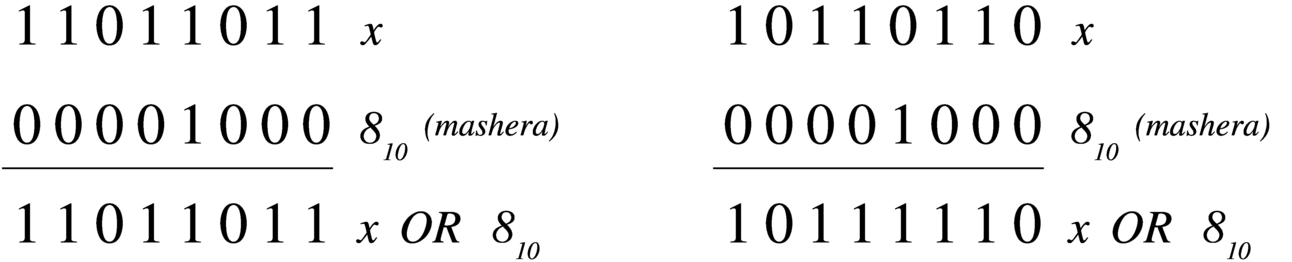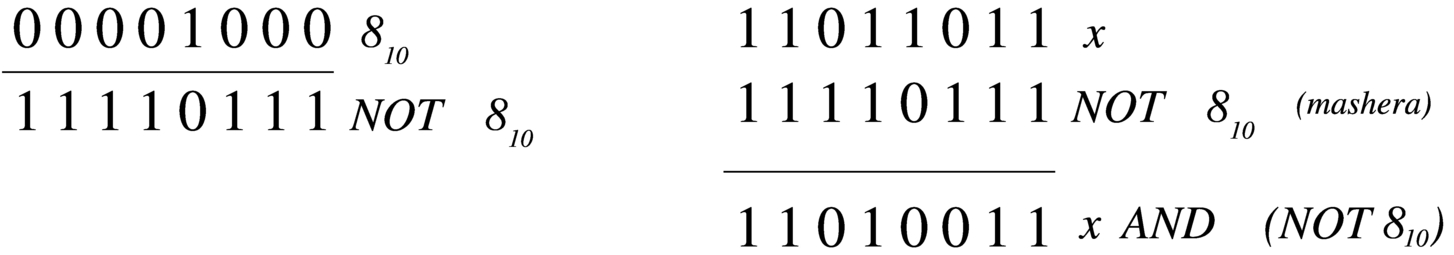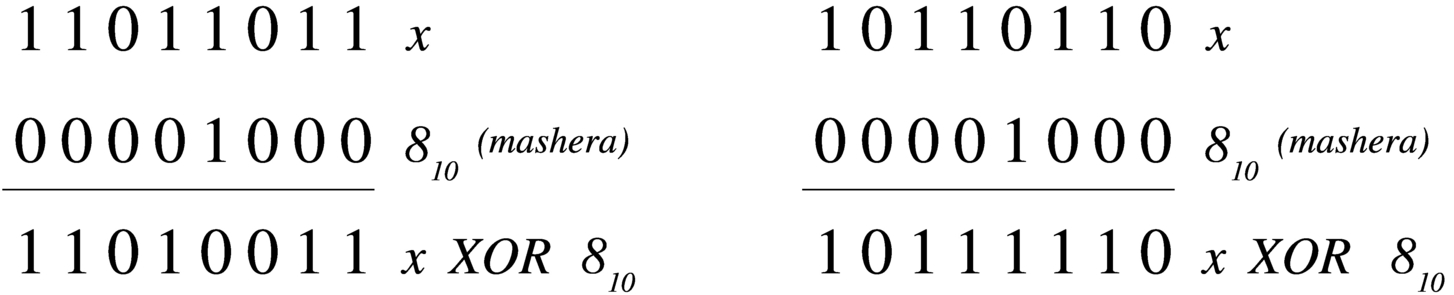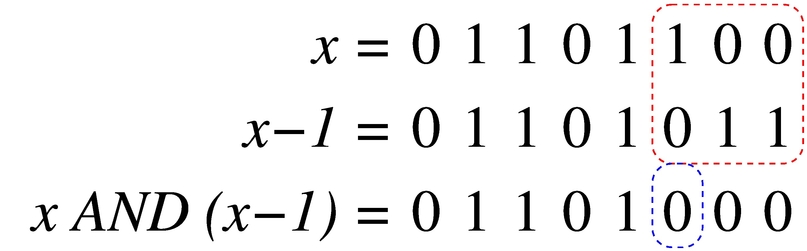successivo
precedente
inizio
fine
indice generale
aiuto
indice analitico
volume
parte
TXT
HTML
PDF
pdf
gdoc
P4
Capitolo 63. Linguaggio macchina
63.1
Organizzazione della memoria
Qui si introduce il problema dell'organizzazione della memoria, da un punto di vista molto vicino a quello della realtà fisica dell'elaboratore. In particolare, viene utilizzata la pseudocodifica, già descritta nella sezione 62.2, per dimostrare in parte il funzionamento e l'utilizzo della pila dei dati, di cui, normalmente, ogni programma dispone.
63.1.1
Pila per salvare i dati
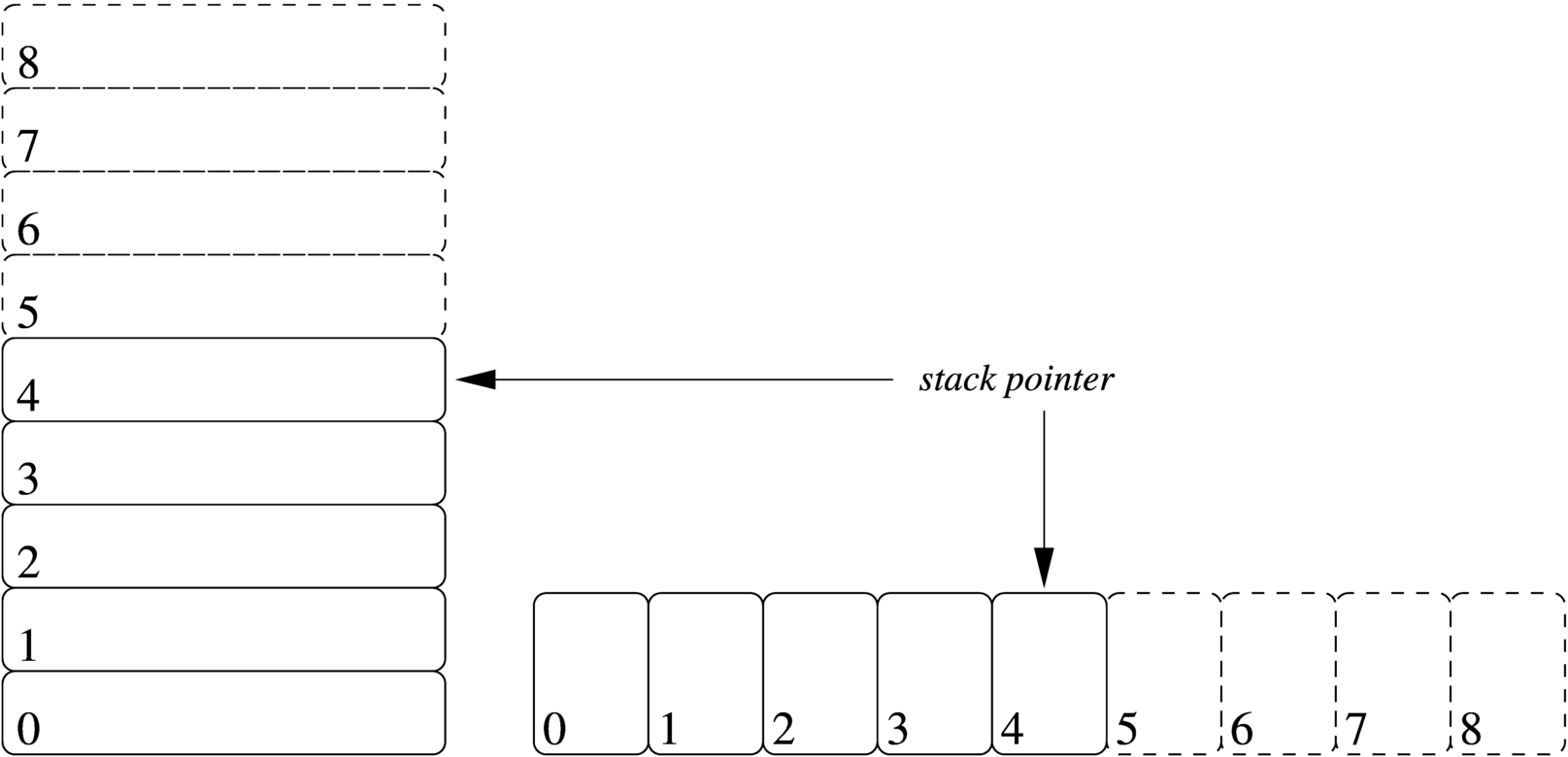
Quando si scrive con un linguaggio di programmazione molto vicino a quello effettivo del microprocessore, si ha normalmente a disposizione una pila di elementi omogenei (stack), usata per accumulare temporaneamente delle informazioni, da espellere poi in senso inverso. Questa pila è gestita attraverso un vettore, dove l'ultimo elemento (quello superiore) è individuato attraverso un indice noto come stack pointer e tutti gli elementi della pila sono comunque accessibili, in lettura e in sovrascrittura, se si conosce la loro posizione relativa.
|
Figura 63.1. Una pila che può contenere al massimo nove elementi, rappresentata nel modo tradizionale, oppure distesa, come si fa per i vettori. Gli elementi che si trovano oltre l'indice (lo stack pointer) non sono più disponibili, mentre gli altri possono essere letti e modificati senza doverli estrarre dalla pila.
|
Per accumulare un dato nella pila (push) si incrementa di una unità l'indice e lo si inserisce in quel nuovo elemento. Per estrarre l'ultimo elemento dalla pila (pop) si legge il contenuto di quello corrispondente all'indice e si decrementa l'indice di una unità.
Tra le altre cose, la pila può servire quando si dispone di una quantità limitata di variabili e si devono accumulare temporaneamente dei valori.
63.1.2
Chiamate di funzioni
I linguaggi di programmazione più vicini alla realtà fisica della memoria di un elaboratore, possono disporre solo di variabili globali ed eventualmente di una pila, realizzata attraverso un vettore, come descritto nella sezione precedente. In questa situazione, la chiamata di una funzione può avvenire solo passando i parametri in uno spazio di memoria condiviso da tutto il programma. Ma per poter generalizzare le funzioni e per consentire la ricorsione, ovvero per rendere le funzioni rientranti, il passaggio dei parametri deve avvenire attraverso la pila in questione.
Per mostrare un esempio iniziale che consenta di comprendere il meccanismo, si può supporre di poter utilizzare delle variabili locali nelle funzioni, mentre per il passaggio dei valori si deve usa la pila. Si vuole trasformare il codice della pseudocodifica seguente in modo da utilizzare tale pila. Si consideri che il programma inizia e finisce nella funzione MAIN(), all'interno della quale si fa la chiamata della funzione SOMMA():
SOMMA (X, Y)
LOCAL Z INTEGER
Z := X + Y
RETURN Z
END SOMMA
MAIN ()
LOCAL A INTEGER
LOCAL B INTEGER
LOCAL C INTEGER
A := 3
B := 4
C := SOMMA (A, B)
END MAIN
|
|
Il programma si trasforma in modo da accumulare nel vettore PILA[] i valori dei parametri della chiamata:
GLOBAL PILA[1000] INTEGER
GLOBAL SP INTEGER
SP := -1
SOMMA ()
LOCAL X := PILA[SP] # Copia il valore del primo
# parametro.
LOCAL Y := PILA[SP - 1] # Copia il valore del
# secondo parametro.
LOCAL Z INTEGER
Z := X + Y
SP++ # Accumula il risultato
PILA[SP] := Z # della somma.
END SOMMA
MAIN ()
LOCAL A INTEGER
LOCAL B INTEGER
LOCAL C INTEGER
A := 3
B := 4
SP++ # Accumula il secondo parametro.
PILA[SP] := B # nella pila.
SP++ # Accumula il primo parametro.
PILA[SP] := A # nella pila.
SOMMA () # Chiama la funzione SOMMA().
C := PILA[SP] #
SP-- # Estrae il risultato.
SP-- # Elimina il primo parametro
# della chiamata.
SP-- # Elimina il secondo parametro
# della chiamata.
END MAIN
|
|
Nella nuova versione della pseudocodifica, la chiamata della funzione SOMMA() è preceduta dall'accumulo nella pila dei parametri, quindi è seguita dall'estrazione del risultato della somma e dall'eliminazione dei due parametri usati nella chiamata (con la sola riduzione del valore dell'indice del vettore). All'interno della funzione SOMMA() si acquisiscono i parametri leggendo i dati corrispondenti dal vettore che li convoglia, sapendo che il primo è nella posizione dell'indice (in quanto è l'ultimo elemento inserito nella pila) e che il secondo è nella posizione precedente. Alla fine, dopo l'esecuzione della somma, il risultato viene inserito nella pila.
L'esempio seguente risolve il problema del calcolo del fattoriale, in modo ricorsivo, seguendo la modalità appena descritta:
GLOBAL PILA[1000] INTEGER
GLOBAL SP INTEGER
SP := -1
FATTORIALE ()
LOCAL X := PILA[SP]
LOCAL W INTEGER
IF X == 1
THEN
SP++ # Accumula il risultato da
PILA[SP] := 1 # restituire, pari a uno.
ELSE
SP++ # Accumula il parametro di
PILA[SP] := X - 1 # chiamata della funzione con
# un valore pari a X - 1.
FATTORIALE ()
W := PILA[SP] # Recupera il risultato
SP-- # della chiamata ricorsiva
# con un valore pari a
# X - 1.
SP-- # Scarica il parametro usato
# per la chiamata.
SP++ # Accumula il risultato del
PILA[SP] := X * W # fattoriale da restituire.
END IF
END FATTORIALE
MAIN ()
LOCAL F INTEGER
F := 7
SP++ # Accumula il valore di cui si
PILA[SP] := F # vuole calcolare il fattoriale.
FATTORIALE () # Calcola il fattoriale.
F := PILA[SP] # Estrae il risultato del
SP-- # fattoriale e scarica il
# valore dalla pila.
SP-- # Scarica la pila del parametro
# usato nella chiamata.
END MAIN
|
|
Se non si possono gestire variabili locali, la pila va usata anche per salvare le variabili che altrimenti verrebbero sovrascritte con la chiamata ricorsiva:
GLOBAL PILA[1000] INTEGER
GLOBAL SP INTEGER
SP := -1
GLOBAL X INTEGER
GLOBAL W INTEGER
FATTORIALE ()
X := PILA[SP]
IF X == 1
THEN
SP++ # Accumula il risultato da
PILA[SP] := 1 # restituire, pari a uno.
ELSE
SP++ # Salva il valore di X nella
PILA[SP] := X # pila.
SP++ # Accumula il parametro di
PILA[SP] := X - 1 # chiamata della funzione
# con un valore pari a X - 1.
FATTORIALE ()
W := PILA[SP] # Recupera il risultato
SP-- # della chiamata ricorsiva
# con un valore pari a
# X - 1.
SP-- # Scarica il parametro usato
# per la chiamata.
X := PILA[SP] # Recupera il valore di X
SP-- # prima della chiamata
# ricorsiva.
SP++ # Accumula il risultato del
PILA[SP] := X * W # fattoriale da restituire.
END IF
END FATTORIALE
...
...
|
|
Come si vede nel nuovo esempio, prima della chiamata ricorsiva viene salvata nella pila solo la variabile X, perché il valore di W non dipende dall'elaborazione e tale variabile riceve un valore utile solo dopo la chiamata in questione. Naturalmente, si comprende che in questo caso particolare, non sarebbe stato nemmeno necessario salvare la variabile X, in quanto il suo valore corretto, dopo la chiamata ricorsiva, lo si può determinare semplicemente reincrementandolo di una unità. Ma qui si è preferito mostrare un esempio molto semplice, risolvendolo in modo generalizzato, anche se ciò non sarebbe necessario.
63.1.3
Funzioni attraverso le istruzioni di salto
Con l'uso di linguaggi di programmazione ragionevolmente evoluti, i salti (go to), condizionati o meno, vanno evitati, dal momento che esistono delle strutture per il controllo del flusso e si può disporre di chiamate di funzioni o procedure. Tuttavia, quando si deve scrivere con un linguaggio molto vicino alla realtà fisica dell'elaboratore, non si dispone più di questi ausilii, o comunque occorre fare i conti con un indice riferito alle istruzioni da eseguire.
In pratica, il programma viene a trovarsi disposto in un vettore, dove un indice serve a sapere qual è l'istruzione successiva da eseguire: instruction pointer. Nel momento in cui si esegue un'istruzione normale, l'indice viene incrementato automaticamente per posizionarsi all'inizio dell'istruzione successiva, mentre in presenza di un'istruzione di salto, l'esecuzione di tale istruzione sposta l'indice nella nuova destinazione.
In queste condizioni, per ottenere ciò che di solito si realizza con delle funzioni ricorsive, occorre gestire l'indice delle istruzioni direttamente. Per la precisione, prima di saltare all'inizio di una funzione, oltre che accumulare i parametri della chiamata nella pila già descritta, occorre accumulare l'indice delle istruzioni, in modo tale da poter riprendere dall'istruzione successiva alla chiamata dopo l'esecuzione di ciò che rappresenta tale funzione.
GLOBAL IP INTEGER # «Instruction pointer»
# (sola lettura).
GLOBAL RETURN INTEGER # Destinazione per il
# ritorno.
...
GLOBAL PILA[1000] INTEGER
GLOBAL SP INTEGER
SP := -1
...
GLOBAL X INTEGER
GLOBAL W INTEGER
...
FATTORIALE ()
X := PILA[SP - 1] # Recupera il primo
# parametro. Si ricorda che
# "PILA[SP]" contiene
# l'indirizzo di ritorno.
IF X == 1
THEN
RETURN := PILA[SP] # Recupera l'indirizzo di
# ritorno.
SP++ # Accumula il risultato da
PILA[SP] := 1 # restituire, pari a uno.
GO_TO RETURN # Torna all'istruzione
# successiva alla chiamata.
ELSE
SP++ # Salva il valore di X nella
PILA[SP] := X # pila.
SP++ # Accumula il parametro di
PILA[SP] := X - 1 # chiamata della funzione
# con un valore pari a X-1.
SP++ # Accumula l'indirizzo
PILA[SP] := IP + 1 # dell'istruzione successiva
# alla prossima.
GO_TO FATTORIALE () # Salta all'inizio della
# funzione.
SP-- # Scarica l'indirizzo di
# ritorno della funzione
# appena conclusa.
W := PILA[SP] # Recupera il risultato
SP-- # della chiamata ricorsiva
# con un valore pari a X-1.
SP-- # Scarica il parametro usato
# per la chiamata.
X := PILA[SP] # Recupera il valore di X
SP-- # prima della chiamata
# ricorsiva.
RETURN := PILA[SP] # Recupera l'indirizzo di
# ritorno.
SP++ # Accumula il risultato del
PILA[SP] := X * W # fattoriale da restituire.
GO_TO RETURN # Torna all'istruzione
# successiva alla chiamata.
END IF
END FATTORIALE
...
...
|
|
Nell'esempio mostrato si considera che la variabile IP sia accessibile in sola lettura e che contenga l'indice dell'istruzione successiva o di quella richiesta da un'istruzione di salto. Prima del salto all'inizio di una funzione, si accumula il valore di IP nella pila, ma incrementandolo di ciò che serve a raggiungere l'istruzione successiva al salto stesso (si suppone che l'incremento di una unità dia il risultato voluto). Nel momento appropriato, il valore dell'indice viene prelevato dalla pila e inserito in una variabile apposita, da usare per saltare alla posizione di ritorno.
63.1.4
Variabili e array
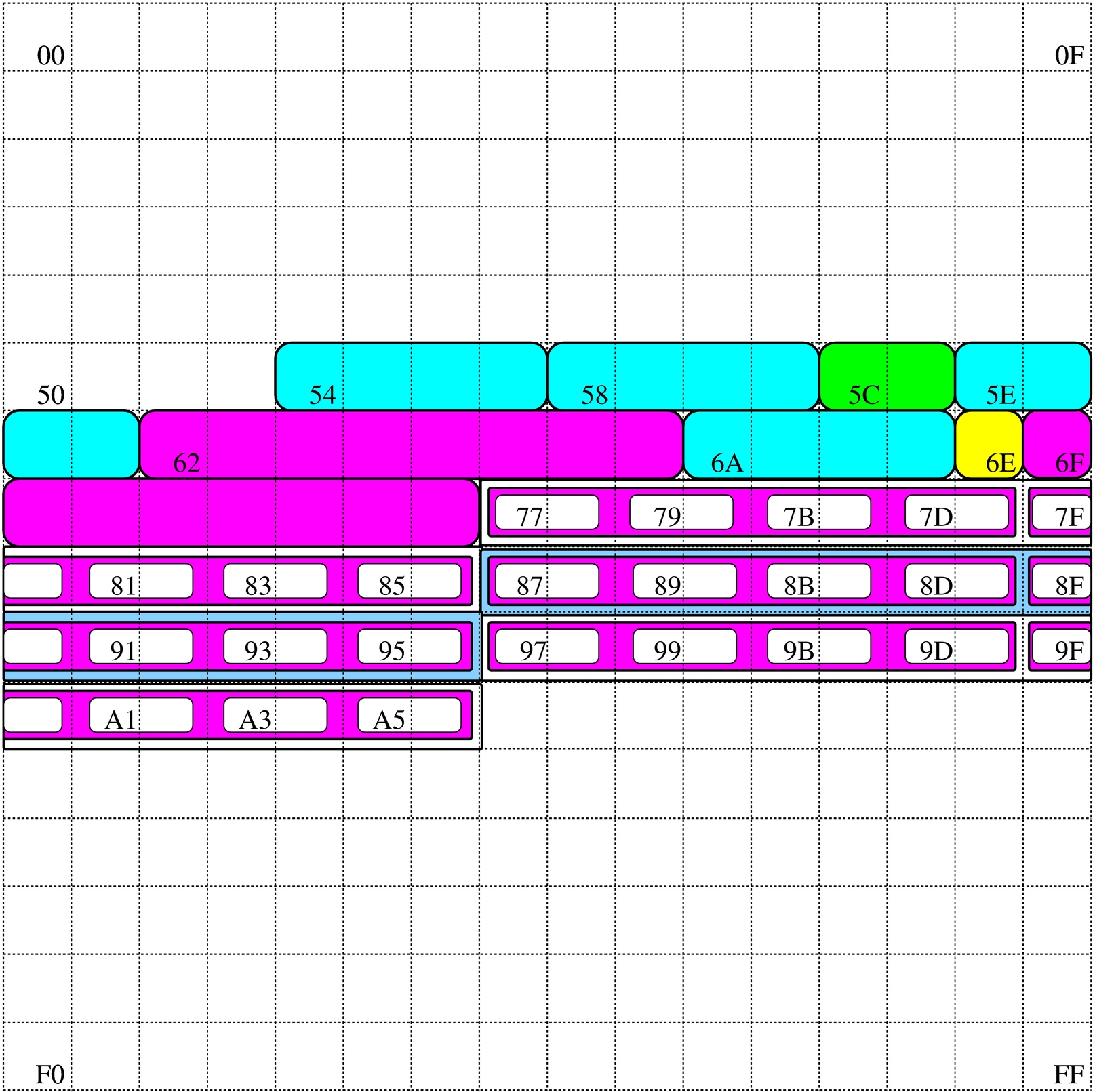
Con un linguaggio di programmazione molto vicino alla realtà fisica dell'elaboratore, la memoria centrale viene vista come un vettore di celle uniformi, corrispondenti normalmente a un byte. All'interno di tale vettore si distendono tutti i dati gestiti, compresa la pila descritta nella sezione 63.1.1. In questo modo, le variabili in memoria si raggiungono attraverso un indirizzo che individua il primo byte che le compone ed è il programma che deve sapere di quanti byte sono composte complessivamente.
|
Figura 63.7. Esempio di mappa di una memoria di soli 256 byte, dove sono evidenziate alcune variabili. Gli indirizzi dei byte della memoria vanno da 0016 a FF16.
|
Nel disegno in cui si ipotizza una memoria complessiva di 256 byte, sono state evidenziate alcune aree di memoria:
| Indirizzo | Dimensione | Indirizzo | Dimensione |
| 5416 | 4 byte | 5816 | 4 byte |
| 5C16 | 2 byte | 5E16 | 4 byte |
| 6216 | 8 byte | 6A16 | 4 byte |
| 6E16 | 1 byte | 6F16 | 8 byte |
|
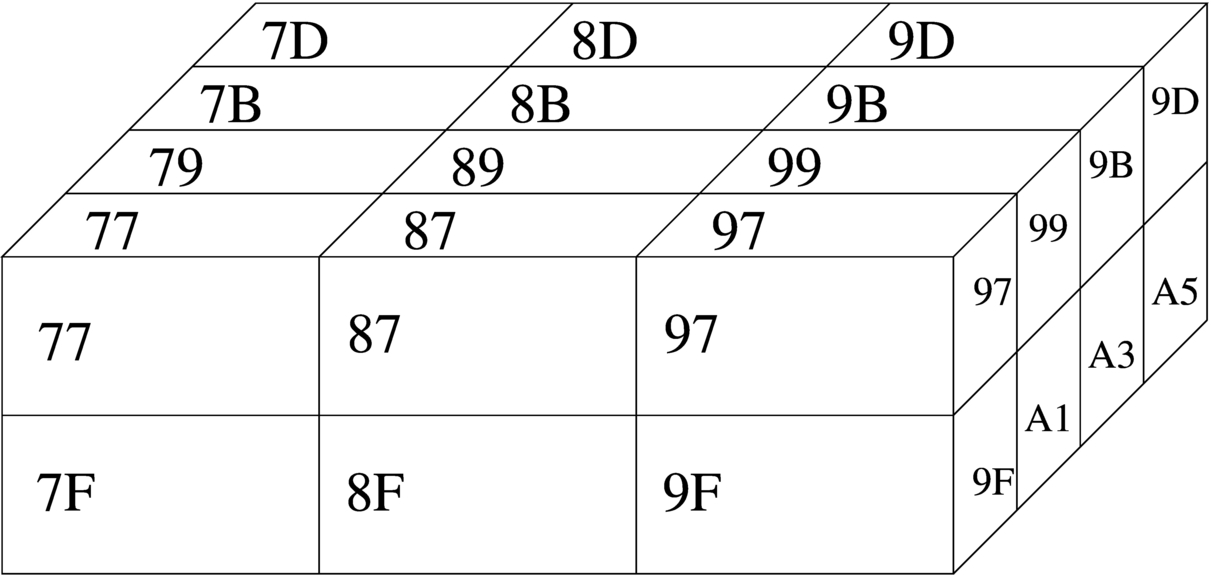
Con una gestione di questo tipo della memoria, la rappresentazione degli array richiede un po' di impegno da parte del programmatore. Nella figura successiva si rappresenta una matrice a tre dimensioni; per ora si ignorino i codici numerici associati alle celle visibili.
|
Figura 63.9. La matrice a tre dimensioni che si vuole rappresentare, secondo un modello spaziale. I numeri che appaiono servono a trovare successivamente l'abbinamento con le celle di memoria utilizzate.
|
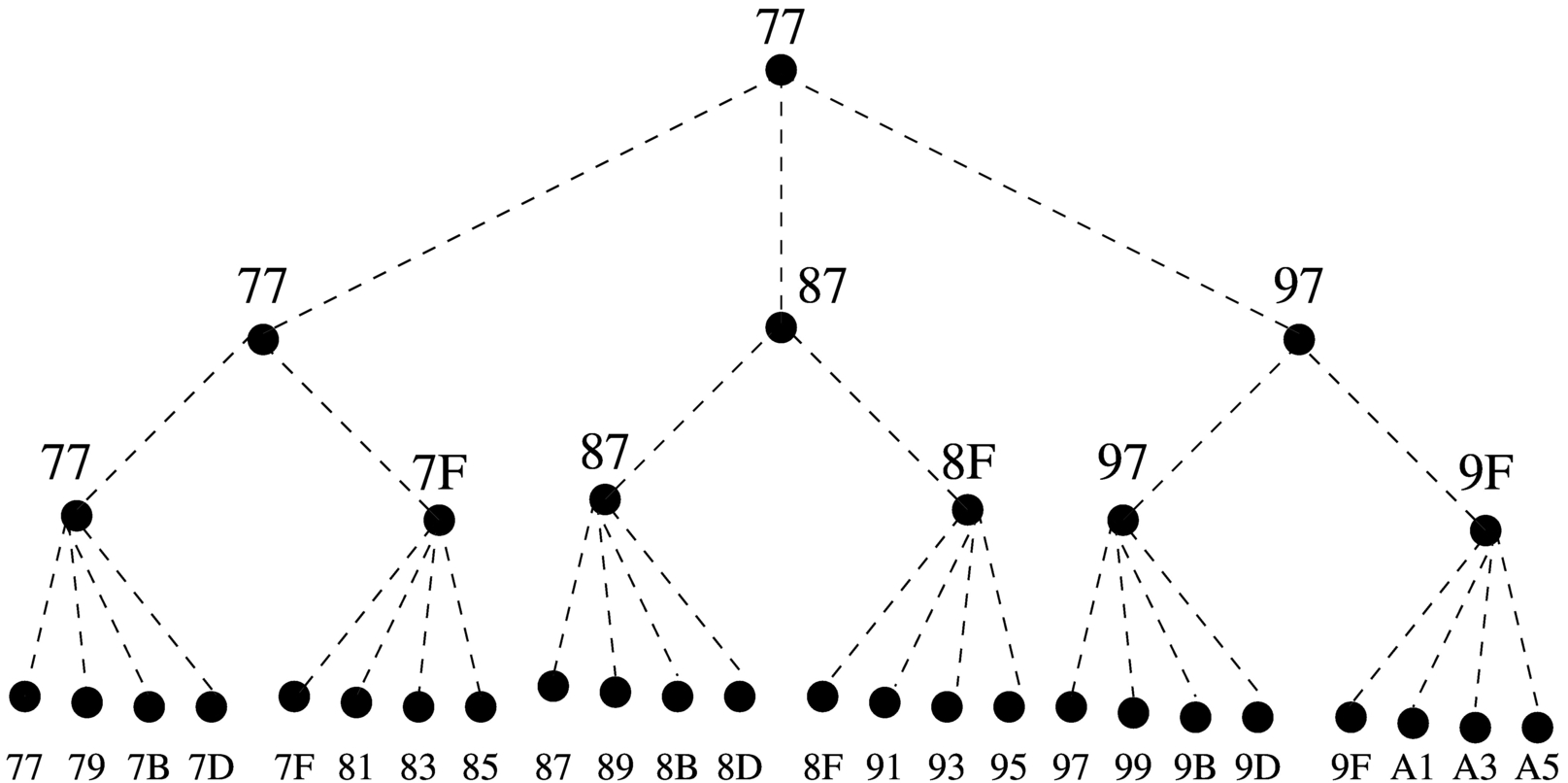
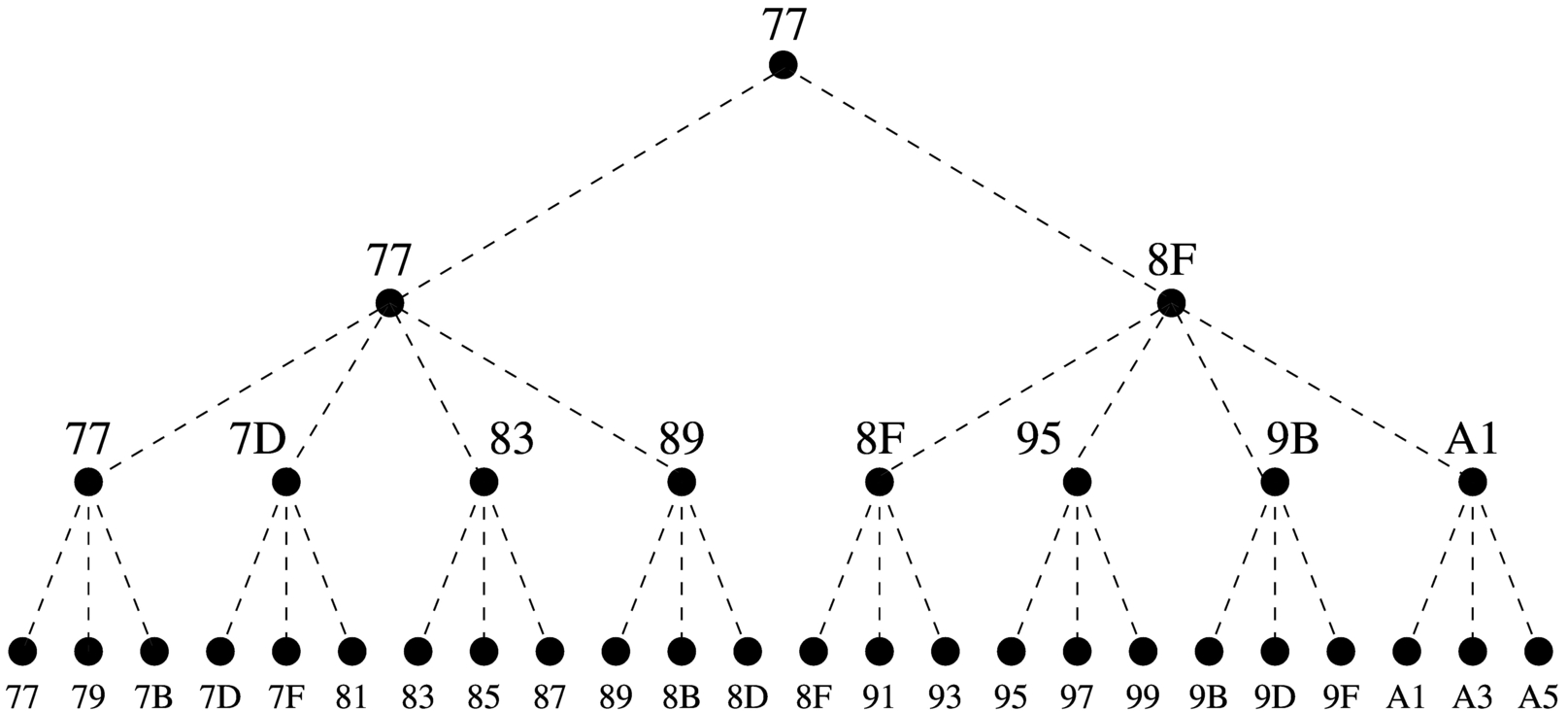
Dal momento che la rappresentazione tridimensionale rischia di creare confusione, quando si devono rappresentare matrici che hanno più di due dimensioni, è più conveniente pensare a strutture ad albero. Nella figura successiva viene tradotta in forma di albero la matrice rappresentata precedentemente.
|
Figura 63.10. La matrice a tre dimensioni che si vuole rappresentare, tradotta in uno schema gerarchico (ad albero).
|
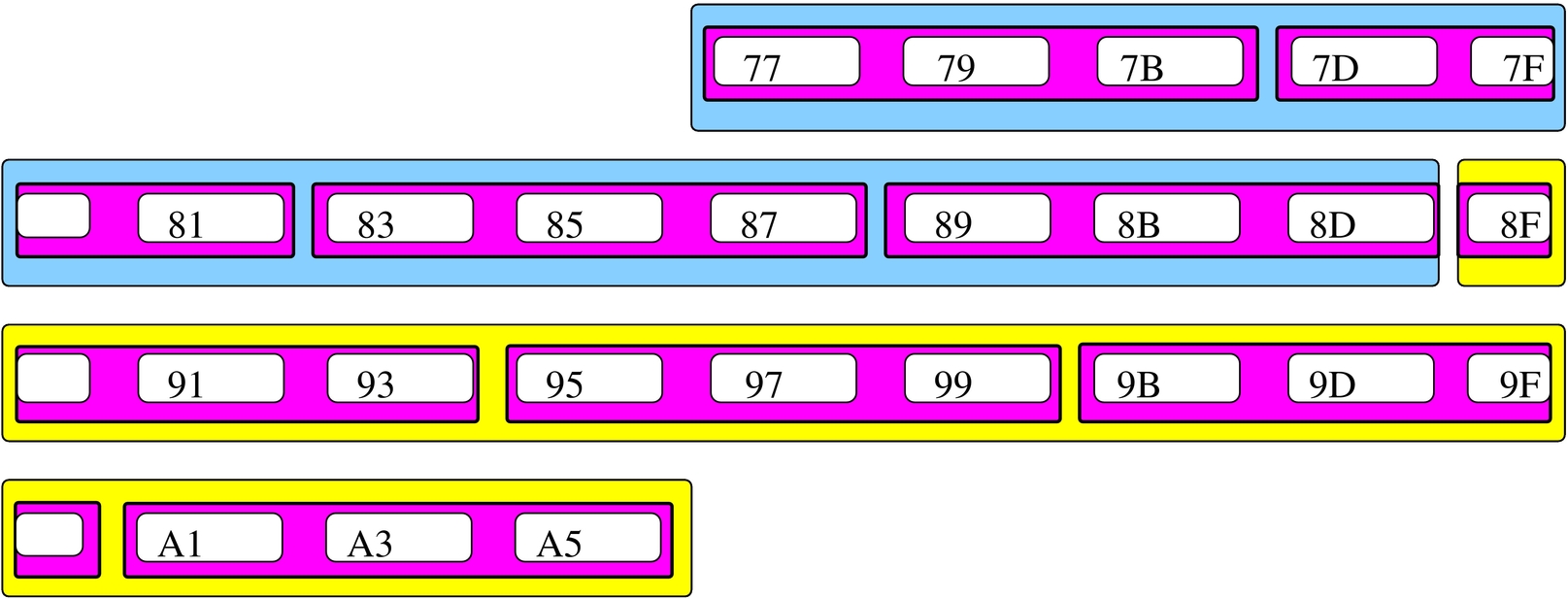
Si suppone di rappresentare la matrice in questione nella memoria dell'elaboratore, dove ogni elemento terminale contiene due byte. Supponendo di allocare l'array a partire dall'indirizzo 7716 nella mappa di memoria già descritta, si potrebbe ottenere quanto si vede nella figura successiva. A questo punto, si può vedere la corrispondenza tra gli indirizzi dei vari componenti dell'array e le figure già mostrate.
|
Figura 63.11. Esempio di mappa di memoria in cui si distende un array che rappresenta una matrice a tre dimensioni con tre elementi contenenti ognuno due elementi che a loro volta contengono quattro elementi da due byte.
|
Si pone quindi il problema di scandire gli elementi dell'array. Considerando che array ha dimensioni «3,2,4» e definendo che gli indici partano da zero, l'elemento [0,0,0] corrisponde alla coppia di byte che inizia all'indirizzo 7716, mentre l'elemento [2,1,3] corrisponde all'indirizzo A516. Per calcolare l'indirizzo corrispondente a un certo elemento occorre usare la formula seguente, dove: le variabili I, J, K rappresentano la dimensioni dei componenti; le variabili i, j, k rappresentano l'indice dell'elemento cercato; la variabile A rappresenta l'indirizzo iniziale dell'array; la variabile s rappresenta la dimensione in byte degli elementi terminali dell'array.
Si vuole calcolare la posizione dell'elemento 2,0,1. Per facilitare i conti a livello umano, si converte l'indirizzo iniziale dell'array in base dieci: 7716 = 11910:
Il valore 15310 si traduce in base sedici in 9916, che corrisponde effettivamente all'elemento cercato: terzo elemento principale, all'interno del quale si cerca il primo elemento, all'interno del quale si cerca il secondo elemento finale.
63.1.5
Gestione alternativa degli indici
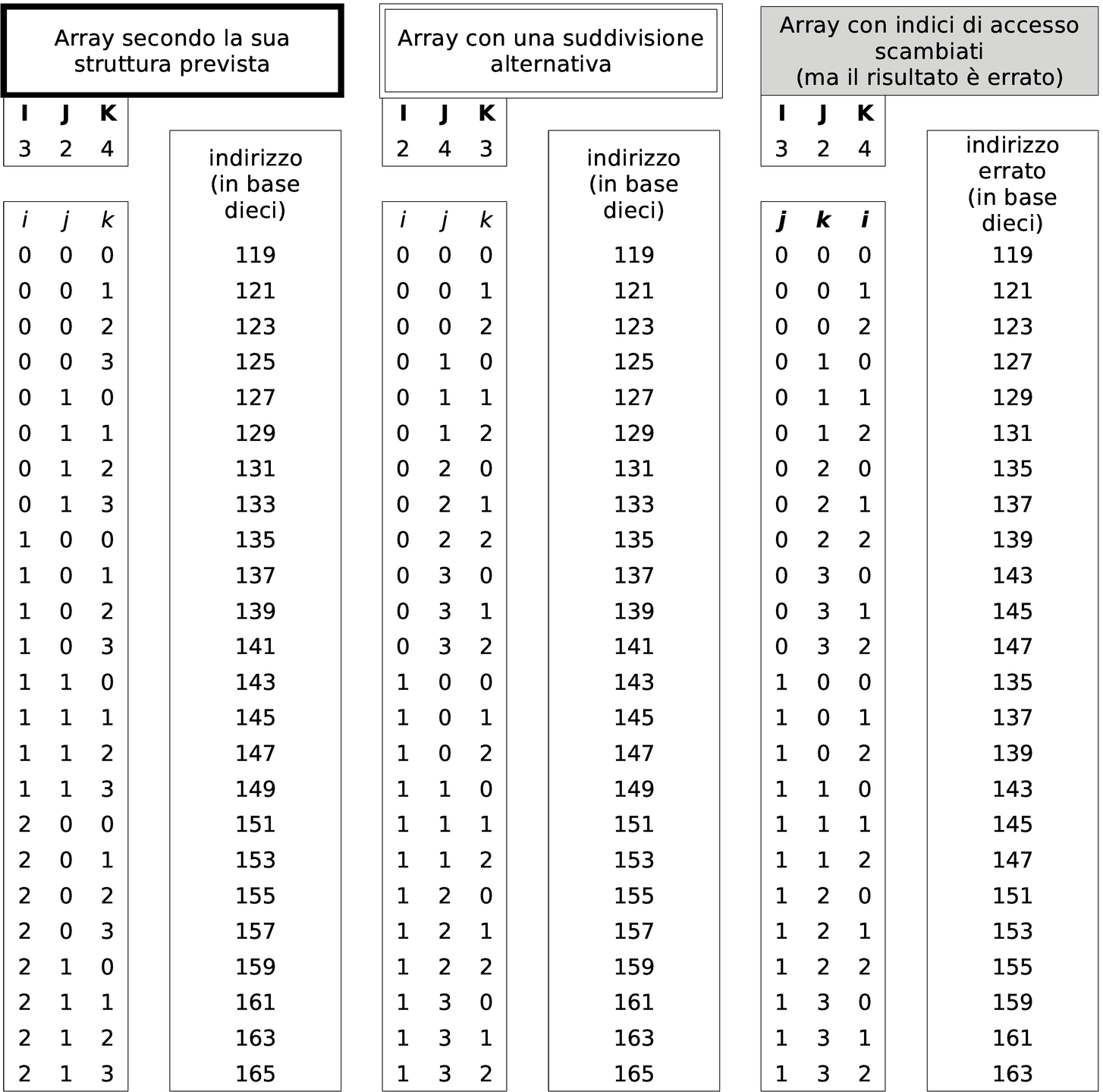
Quando si vuole disporre un array nella memoria, se quello che conta è solo raggiungere gli elementi terminali che lo compongono, non fa molta differenza se la gerarchia con cui si organizza è diversa. Per esempio, l'array che prima era strutturato in elementi di dimensione 3,2,4, potrebbe benissimo essere definito secondo la suddivisione 4,3,2, gestendo di conseguenza gli indici. Lo si può vedere nella figura successiva che riproduce la nuova gerarchia in forma di albero.
|
Figura 63.15. La stessa matrice, ma organizzata secondo una gerarchia differente.
|
Nella figura successiva si riprende l'esempio di mappa della memoria, dove l'array già apparso nella sezione precedente è disposto secondo la nuova suddivisione.
|
Figura 63.16. La nuova mappa della memoria.
|
Nella tabella successiva si mettono a confronto le coordinate calcolate per raggiungere gli elementi dell'array strutturato secondo le due gerarchie mostrate (quella della sezione precedente e quella attuale). Si può vedere che le celle di memoria vengono raggiunte nello stesso modo (nella tabella gli indirizzi sono annotati in base dieci). Viene anche mostrato cosa può accadere se si usano gli indici di accesso in modo non coincidente alla gerarchia prescelta.
|
Tabella 63.17. Confronto dell'indirizzamento della memoria utilizzando due modi diversi di organizzare gli elementi dell'array, con un esempio di cosa accade quando gli indici non combaciano con la struttura scelta.
|
63.1.6
Ordine dei byte
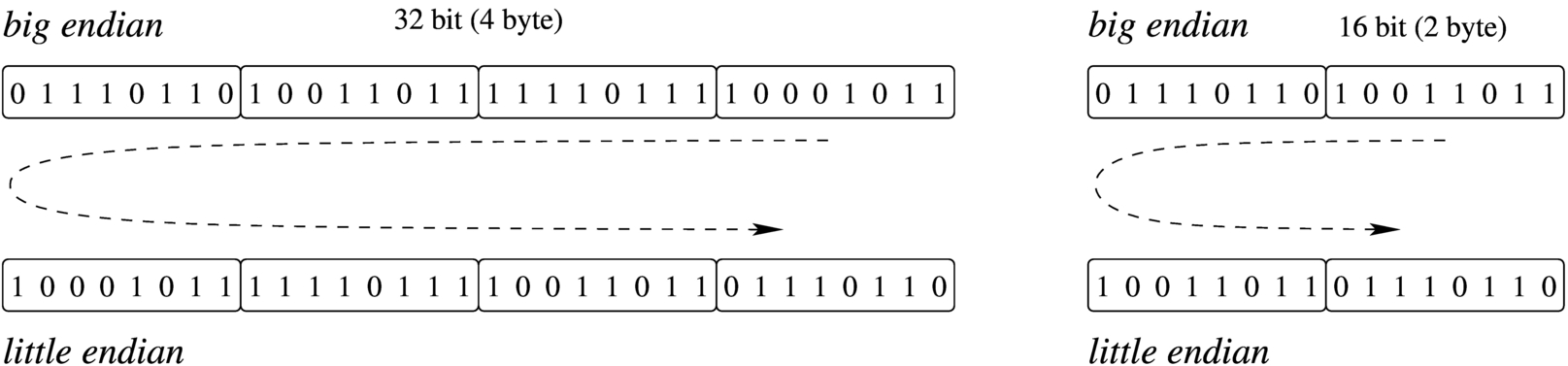
Come già descritto, normalmente l'accesso alla memoria avviene conoscendo l'indirizzo iniziale dell'informazione cercata, sapendo poi per quanti byte questa si estende. Il microprocessore, a seconda delle proprie caratteristiche e delle istruzioni ricevute, legge e scrive la memoria a gruppetti di byte, più o meno numerosi. Ma l'ordine dei byte che il microprocessore utilizza potrebbe essere diverso da quello che si immagina di solito.
|
Figura 63.18. Confronto tra big endian e little endian.
|
A questo proposito, per quanto riguarda la rappresentazione dei dati nella memoria, si distingue tra big endian, corrispondente a una rappresentazione «normale», dove il primo byte è quello più significativo (big), e little endian, dove la sequenza dei byte è invertita (ma i bit di ogni byte rimangono nella stessa sequenza standard) e il primo byte è quello meno significativo (little). La cosa importante da chiarire è che l'effetto dell'inversione nella sequenza porta a risultati differenti, a seconda della quantità di byte che compongono l'insieme letto o scritto simultaneamente dal microprocessore, come si vede nella figura.
63.1.7
Stringhe, array e puntatori
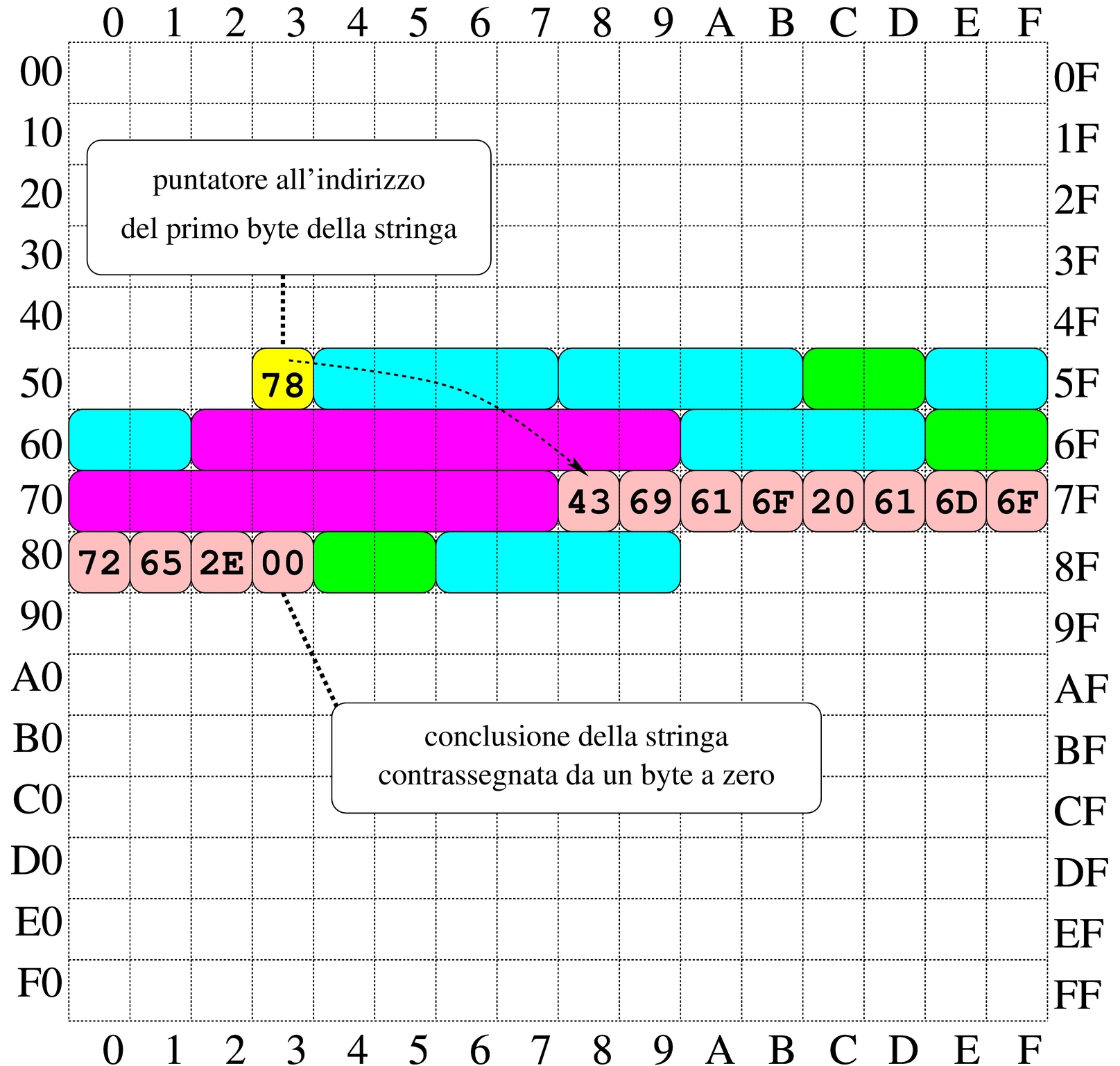
Le stringhe sono rappresentate in memoria come array di caratteri, dove il carattere può impiegare un byte o dimensioni multiple (nel caso di UTF-8, un carattere viene rappresentato utilizzando da uno a quattro byte, a seconda del punto di codifica raggiunto). Il riferimento a una stringa viene fatto come avviene per gli array in generale, attraverso un puntatore all'indirizzo della prima cella di memoria che lo contiene; tuttavia, per non dovere annotare la dimensione di tale array, di norma si conviene che la fine della stringa sia delimitata da un byte a zero, come si vede nell'esempio della figura.
|
Figura 63.19. Stringa conclusa da un byte a zero (zero terminated string), a cui viene fatto riferimento per mezzo di una variabile che contiene il suo indirizzo iniziale. La stringa contiene il testo Ciao amore., secondo la codifica ASCII.
|
Nella figura si vede che la variabile scalare collocata all'indirizzo 5316 contiene un valore da intendere come indirizzo, con il quale si fa riferimento al primo byte dell'array che rappresenta la stringa (in posizione 7816). La variabile collocata in 5316 assume così il ruolo di variabile puntatore e, secondo il modello ridotto di memoria della figura, è sufficiente un solo byte per rappresentare un tale puntatore, dal momento che servono soltanto valori da 0016 a FF16.
63.1.8
Utilizzo della memoria
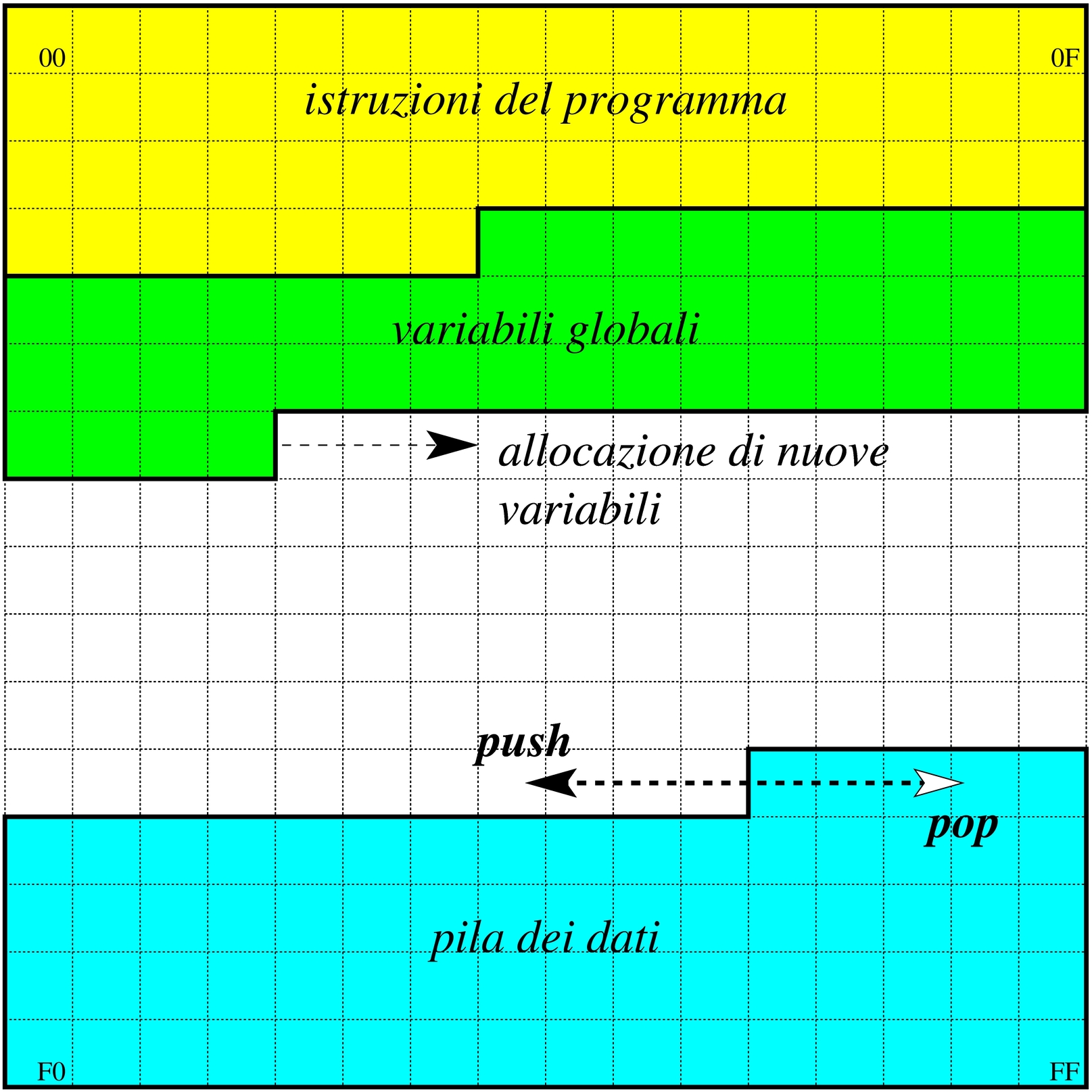
La memoria dell'elaboratore viene utilizzata sia per contenere i dati, sia per il codice del programma che li utilizza. Ogni programma ha un proprio spazio in memoria, che può essere reale o virtuale; all'interno di questo spazio, la disposizione delle varie componenti potrebbe essere differente. Nei sistemi che si rifanno al modello di Unix, nella parte più «bassa» della memoria risiede il codice che viene eseguito; subito dopo vengono le variabili globali del programma, mentre dalla parte più «alta» inizia la pila dei dati che cresce verso indirizzi inferiori. Si possono comunque immaginare combinazioni differenti di tale organizzazione, pur rispettando il vincolo di avere tre zone ben distinte per il loro contesto (codice, dati, pila); tuttavia, ci sono situazioni in cui i dati si trovano mescolati al codice, per qualche ragione.
|
Figura 63.20. Esempio di disposizione delle componenti di un programma in esecuzione in memoria, secondo il modello Unix.
|
63.2
Architettura, linguaggio, contesto virtuale, terminologia
Ciò che un microprocessore esegue sono istruzioni in linguaggio macchina, composte secondo la sintassi che il microprocessore stesso è in grado di interpretare. Il linguaggio macchina è fatto esclusivamente di numeri (da gestire in base due) e per questo, di norma, non viene utilizzato direttamente a livello umano.
Quando si deve intervenire al livello più basso possibile della programmazione, ci si avvale generalmente di un linguaggio «assemblatore» (assembly), ovvero un linguaggio che, pur rimanendo legato alle caratteristiche del microprocessore e in generale a quelle dell'architettura dell'elaboratore, esprime le istruzioni in una forma simbolica più comprensibile. Naturalmente, un programma scritto secondo un linguaggio assemblatore deve essere elaborato da un compilatore (assembler) per generare il linguaggio macchina effettivo.
Non esiste un'architettura standard, né un linguaggio macchina standard e di conseguenza non esiste nemmeno un linguaggio assemblatore standard. Un programma scritto con un linguaggio assemblatore adatto a un certo tipo di architettura non può funzionare in un'architettura differente. Pertanto, se si usa un tale linguaggio, lo si fa soprattutto per quelle cose che altrimenti non potrebbero essere risolte (come il codice necessario all'avvio del sistema operativo).
63.2.1
Memoria e registri
Le architetture per elaboratore più diffuse prevedono un microprocessore in grado di comunicare con una memoria centrale, organizzata come un vettore di celle, contenenti una quantità uniforme di bit, accessibili attraverso un indice che ne rappresenta l'indirizzo. Oltre a questo, il microprocessore dispone internamente di alcuni registri, ovvero delle celle singole di memoria con compiti più o meno specializzati.
La dimensione dei registri condiziona la capacità del microprocessore di eseguire dei calcoli e la capacità di indirizzamento della memoria. La dimensione dei registri più comuni di un microprocessore corrisponde alla dimensione della parola (word).
Generalmente, la memoria centrale è organizzata in celle di byte (intesi come gruppi di otto bit), ma possono esistere architetture in cui tali celle corrispondono alla dimensione della parola del microprocessore, o anche altre dimensioni, ma in generale una cella della memoria deve essere contenibile in un registro.
Nella memoria centrale devono risiedere sia i dati da elaborare, sia le istruzioni in linguaggio macchina. Pertanto, un registro molto importante in un microprocessore è quello che tiene traccia, nella memoria centrale, dell'istruzione successiva da eseguire: instruction pointer o program counter.
Nel caso degli elaboratori x86-32, l'architettura più comune negli anni 1990 prevede parole da 32 bit e una memoria organizzata in byte; pertanto è possibile gestire lo spazio di 4 Gibyte (232). Purtroppo, nella documentazione originale di questo tipo di architettura si usa il termine word per identificare una dimensione a 16 bit, come era nel primo microprocessore di quella serie (8088/8086), per motivi di compatibilità.
63.2.2
Indicatori o «flag»
Un indicatore, ovvero un flag, è un'informazione costituita da un solo valore binario (Vero o Falso) che serve a tenere traccia dell'esito delle operazioni svolte all'interno del microprocessore. In generale, gli indicatori sono raccolti assieme in un registro specializzato.
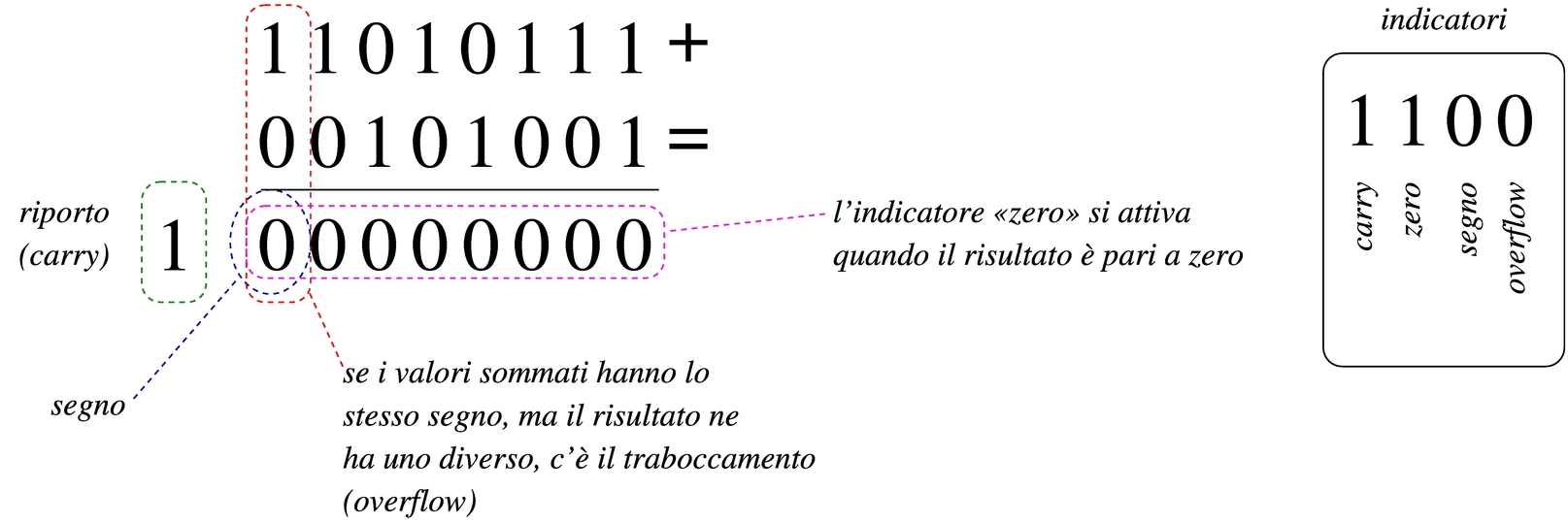
Gli indicatori più importanti in assoluto sono due: «riporto» o carry che serve a conoscere l'esito delle somme (e delle sottrazioni) di valori senza segno; «traboccamento» o overflow che serve a conoscere l'esito delle somme (e delle sottrazioni) di valori con segno. Bisogna osservare che, tra le varie architetture, non è detto che gli indicatori funzionino sempre nella stessa maniera.
|
Tabella 63.21. Indicatori comuni tra le varie architetture.
Indicatore
(flag) | Descrizione |
| carry | È l'indicatore del riporto che diventa utile per le operazioni con valori senza segno. |
| borrow | È l'indicatore della richiesta del prestito di una cifra nelle sottrazioni che diventa utile per le operazioni con valori senza segno. Di solito questo indicatore è costituito dallo stesso carry, il cui risultato va inteso in questo senso quando si eseguono delle sottrazioni. |
| overflow | È l'indicatore di traboccamento per le operazioni che riguardano valori con segno. |
| zero | Viene impostato dopo un'operazione che dà come risultato il valore zero. |
| sign | In linea di massima, riproduce il bit più significativo di un valore, dopo un'operazione. Se il valore è da intendersi con segno, l'indicatore serve a riprodurre il segno stesso. |
| parity | In linea di massima, si attiva quando l'ultima operazione produce un risultato contenente una quantità pari di bit a uno (ma ciò non significa che il valore corrispondente sia pari). |
|
63.2.3
«Opcode»
Nel linguaggio macchina, il codice numerico che descrive le istruzioni è definito operation code (codice operazione) e si abbrevia come opcode (o solo «op»). La lunghezza complessiva dell'istruzione può cambiare a seconda degli operandi che il codice di operazione prevede di avere.
63.2.4
Accesso alla memoria
Le istruzioni fornite al microprocessore (in linguaggio macchina o secondo la simbologia del linguaggio assemblatore) contengono dati o riferimenti a dei dati. A questo proposito, ogni architettura definisce le proprie tipologie e, di conseguenza, non esiste una denominazione uniforme.
Spesso si distingue tra le modalità di indirizzamento riferite al codice del programma, rispetto a quelle relative ai dati veri e propri. Le forme di indirizzamento più semplici riferite al codice possono essere assolute, quando si specifica un indirizzo preciso, oppure relative, quando si specifica uno spostamento relativo dalla posizione corrente. Si usa l'indirizzamento al codice con i salti e con le chiamate di subroutine. L'indirizzamento ai dati potrebbe comprendere le forme dell'elenco seguente:
-
valori numerici costanti, incorporati nell'istruzione, che spesso sono chiamati «immediati»;
-
registri da intendere come tali;
-
aree di memoria indicate direttamente con un indirizzo;
-
aree di memoria indicate da un indirizzo composto da un valore di riferimento e l'aggiunta di un indice o di uno scostamento;
-
aree di memoria indicate attraverso un registro che ne contiene l'indirizzo;
-
aree di memoria indicate con un indirizzo composto dalla somma tra un valore costante, il contenuto di un registro ed eventualmente uno scostamento.
|
In generale, il termine «valore immediato» si riferisce a un'informazione numerica costante, incorporata nell'istruzione in linguaggio macchina. Ogni volta che si indica un riferimento fisso alla memoria (di solito lo si fa attraverso un «simbolo», rappresentato da etichetta, che il compilatore traduce in un indirizzo, in uno scostamento o in un dislocamento), sia per ciò che riguarda il codice, sia per i dati veri e propri, si sta utilizzando un valore immediato, anche se è compito del compilatore tradurlo effettivamente in un numero. Tale valore è «immediato» in quanto il microprocessore non deve eseguire alcun calcolo per interpretarlo.
|
Come si può intuire, le forme più complesse di rappresentazione delle variabili in memoria consentono una scansione utile per rappresentare gli array di dati.
È però importante distinguere i contesti: un conto è l'istruzione macchina, un altro è l'istruzione scritta nel linguaggio assemblatore. Generalmente gli indirizzi della memoria non vengono scritti materialmente in forma numerica, lasciando che sia il compilatore a tradurli nella realtà concreta. Ma questo comporta spesso anche la scelta di un tipo di istruzione macchina rispetto a un altro, in base al contesto, cosa che rimane sempre a carico del compilatore. D'altro canto, certi tipi di indirizzamento complesso, vengono elaborati e semplificati dal compilatore stesso.
È importante sottolineare che le istruzioni in linguaggio macchina (opcode) possono essere diverse, anche se riferite a uno stesso tipo di operazione, quando cambia l'entità di un dislocamento o il tipo di indirizzamento; pertanto, quando si legge il manuale di riferimento per un certo microprocessore, si trova l'elenco delle istruzioni e la descrizione degli operandi previsti, ma non è detto che nel linguaggio assemblatore si debba usare esattamente la stessa modalità.
63.2.5
Modello della memoria nei sistemi Unix(1)
Nei sistemi Unix, inclusi i sistemi liberi che si rifanno a quel modello tradizionale, i processi elaborativi vedono la memoria come un solo vettore contenente: le istruzioni da eseguire, lo spazio previsto per i dati e una pila, utilizzata sostanzialmente nel modo descritto nelle sezioni precedenti. La pila inizia però da una posizione elevata di questo vettore e si espande in posizioni inferiori. Pertanto, l'indice della pila viene decrementato quando la si carica di un nuovo elemento (push) e viene incrementato quando invece la si scarica (pop). Ciò è come dire che la pila è rovesciata e si estende «verso il basso».
|
Figura 63.22. Semplificazione del modo in cui un processo elaborativo Unix vede la memoria. La dimensione della memoria virtuale a disposizione di un processo elaborativo dipende normalmente dall'architettura dell'elaboratore; il valore indicato nel disegno serve solo come semplificazione. A sinistra si vedono gli indirizzi di memoria partire dal basso ed estendersi in altro; a destra si vede l'opposto. Nella seconda forma visuale la pila cresce «dal basso», ma rimane il fatto che il modo di gestire l'indice sia lo stesso.
|
La rappresentazione che si vede nella parte sinistra della figura è quella tradizionale, ma se si ragiona «in senso di lettura», potrebbe essere più logico rappresentare gli indirizzi più bassi in altro, progredendo verso il basso. In tal caso, la pila si estende come si è abituati normalmente a pensarla, ma resta il fatto che l'indice di gestione della pila deve essere decrementato per aggiungere degli elementi sulla stessa.
63.2.6
Sintassi «AT&T» e «Intel»
Quando si utilizza l'architettura x86 si trovano generalmente compilatori per linguaggi assemblatori di due tipi: uno conforme allo stile usato nei sistemi Unix del PDP-11; l'altro conforme alla simbologia usata dalla documentazione della casa produttrice dei primi microprocessori di questo tipo. Dal momento che Unix è nato nei laboratori Bell AT&T, la prima notazione è nota come «sintassi AT&T»; per converso, l'altra è la «sintassi Intel».
Generalmente, negli ambienti legati ai sistemi Unix e simili, GNU/Linux incluso, si preferisce usare compilatori con sintassi AT&T.
63.2.7
Macchina virtuale
Quando si scrive un programma in linguaggio assemblatore, occorre tenere in considerazione il contesto di funzionamento. Di norma questo contesto è dato dal sistema operativo, attraverso il quale il programma viene caricato in memoria e poi eseguito.
|
In effetti, l'uso diretto di un linguaggio assemblatore è appropriato quando si opera al di fuori del sistema operativo, per esempio, proprio per il codice di avvio di un sistema. Tuttavia, quando si inizia lo studio di un tale linguaggio, i programmi che si realizzano sono fatti per un sistema già funzionante che quindi si sottomettono al controllo di questo.
|
L'ambiente in cui si trova a funzionare il programma avviato attraverso il sistema operativo è una macchina virtuale che può avere caratteristiche differenti rispetto alla «macchina reale», soprattutto per ciò che riguarda l'indirizzamento della memoria e per le funzioni a cui è possibile accedere.
63.2.8
Compilazione e collegamento
Nei sistemi operativi che si rifanno al modello di Unix, la compilazione di un programma scritto secondo un linguaggio assemblatore segue un procedimento comune. Una prima fase interpreta un file sorgente e produce un file «oggetto», ripetendo eventualmente il procedimento per altri file che servono a produrre lo stesso programma. I file oggetto ottenuti in questa fase sono file binari che non sono ancora pronti per essere eseguiti, in quanto alcune informazioni sono rimaste da definire. Nella seconda fase (nota come link) i file oggetto che servono a comporre un certo programma vengono collegati assieme, generando il file eseguibile vero e proprio.
In pratica, un programma eseguibile viene ottenuto da almeno un file oggetto, ma spesso i file oggetto che servono a produrre un programma sono più di uno. Infatti, nei file che costituiscono i sorgenti possono esserci dei riferimenti a zone di memoria e a funzioni descritte in altri file, pertanto è compito della fase di «collegamento» il comporre assieme i file oggetto in modo che questi riferimenti reciproci vengano consolidati.
Secondo la tradizione, in modo predefinito, il compilatore di un linguaggio assemblatore genera il file oggetto con il nome a.out, ma anche il linker, ovvero il programma che collega assieme i file oggetto, creerebbe un file eseguibile con lo stesso nome (naturalmente, di solito si dichiara esplicitamente il nome del file da generare). È bene sapere che il nome «a.out» deriva dalle primissime edizioni di Unix e significa Assembler output.
Quando si usano linguaggi di programmazione più evoluti rispetto al codice che si rifà direttamente alle caratteristiche del microprocessore, spesso il procedimento di compilazione passa per la produzione di un sorgente in linguaggio assemblatore, che poi viene compilato secondo la modalità consueta. In ogni caso, se la compilazione prevede la produzione intermedia di file oggetto, teoricamente, questi possono essere collegati assieme ad altri file oggetto prodotti da altri linguaggi. Perché ciò sia possibile effettivamente, occorre comunque che siano compatibili nel modo di condividere la memoria e di eseguire le chiamate delle funzioni, al livello del linguaggio macchina.
Rimane da tenere presente che i file oggetto e i file eseguibili hanno un formato definito da un certo standard. Di questi standard ne esistono molti, anche se nei sistemi Unix e simili si è affermato prevalentemente il formato ELF (Executable and linkable format). I primi formati usati nei sistemi Unix sono noti con come «a.out», confondendosi con il nome del file generato in modo predefinito dal compilatore. Si osservi che i compilatori attuali, in mancanza di altre indicazioni, producono file con il nome a.out, indipendentemente dal formato che questi hanno, formato che può benissimo essere ELF o altro.
63.3
Rappresentazione di valori numerici
La memoria di un elaboratore consente di annotare esclusivamente delle cifre binarie e in uno spazio di dimensione prestabilita e fissa. Nelle sezioni successive si descrivono alcune forme di rappresentazione dei valori numerici, nell'ambito di queste limitazioni.
63.3.1
Codifica delle singole cifre
Un valore numerico potrebbe essere espresso come una stringa di caratteri, corrispondenti alle cifre numeriche che lo rappresentano secondo la notazione in base dieci. Naturalmente, una rappresentazione del genere implica uno spreco di spazio nel sistema di memorizzazione e richiede una trasformazione prima di poter procedere all'esecuzione di calcoli numerici.
Esistono diverse forme di rappresentazioni numeriche, intese come sequenze di cifre in base dieci, che utilizzano quattro bit per ogni cifra. Il sistema più comune è noto con il nome BCD: Binary coded decimal.
I sistemi di rappresentazione numerica che utilizzano quattro bit per ogni cifra di un valore in base dieci, si utilizzano per esempio nel linguaggio COBOL, per le variabili scalari di tipo computational.
|
Tabella 63.23. Alcune codifiche per la rappresentazione di cifre numeriche (in base dieci) a gruppi di quattro bit.
Cifra
decimale | Codice BCD (8421) | Codice «eccesso 3» | Codice 2421 | Codice 5211 | Codice 631-1 | Codice 732-1 |
| 0 | 00002 | 00112 | 00002 | 00002 | 00002
00112 | 00002 |
| 1 | 00012 | 01002 | 00012 | 00012
00102 | 00102 | 00112 |
| 2 | 00102 | 01012 | 00102
10002 | 01002
00112 | 01012 | 00102 |
| 3 | 00112 | 01102 | 00112
10012 | 01012
01102 | 01002 | 01002 |
| 4 | 01002 | 01112 | 01002
10102 | 01112 | 01102 | 01112 |
| 5 | 01012 | 10002 | 01012
10112 | 10002 | 10012 | 01102 |
| 6 | 01102 | 10012 | 01102
11002 | 10102
10012 | 10002 | 10012 |
| 7 | 01112 | 10102 | 01112
11012 | 10112
11002 | 10102 | 10002 |
| 8 | 10002 | 10112 | 11102 | 11102
11012 | 11012 | 10112 |
| 9 | 10012 | 11002 | 11112 | 11112 | 11002
11112 | 10102 |
|
La codifica BCD e altre sono codici pesati, in quanto a ogni bit viene attribuito un peso, da sommare per determinare il valore. I pesi per la codifica BCD sono 8, 4, 2 e 1; pertanto, il codice BCD 10012 corrisponde a 1*8+0*4+0*2+1*1 = 9. Nella tabella riepilogativa, i codici pesati sono: BCD, 2421, 5211, 631-1 e 732-1. I nomi usati per questi codici sono costituiti dalla sequenza dei pesi stessi.
Alcuni codici pesati prevedono la rappresentazione di qualche cifra in più in un modo alternativo. Per esempio, nel codice 2421, il numero due si può ottenere sia come 10002, sia come 00102.
I codici pesati come BCD (ovvero 8421), 2421 e 5211, prevedono pesi positivi; i codici come 631-1 e 732-1, prevedono anche pesi negativi. Per esempio, con il codice 732-1, si ottiene il valore uno con il codice 00112, perché il secondo bit (a destra) vale come il numero due, mentre il primo bit (a destra) sottrae una unità.
Dei codici che appaiono nella tabella, il codice a eccesso tre, non è un codice pesato, in quanto corrisponde al codice BCD, a cui si aggiunge il valore tre.
|
È necessario sottolineare che il codice BCD, a seconda del contesto, può essere riferito anche a un codice a otto bit, dove i primi quattro, più significativi, sono posti a zero.
|
63.3.2
Rappresentazione binaria di numeri interi senza segno
Quando si rappresentano dei valori numerici in forma binaria, senza passare per una conversione di ogni singola cifra decimale, si usa tutta la sequenza di bit per il valore. La rappresentazione di un valore intero senza segno coincide normalmente con il valore binario contenuto nella variabile. Pertanto, una variabile della dimensione di 8 bit, può rappresentare valori da zero a 28-1:
000000002 (010)
000000012 (110)
000000102 (210)
...
111111102 (25410)
111111112 (25510)
63.3.3
Rappresentazioni binarie superate di numeri interi con segno
Un numero binario, inserito nella memoria di un elaboratore, può contenere esclusivamente cifre numeriche; pertanto, la rappresentazione del segno può avvenire solo attraverso cifre numeriche. A partire approssimativamente dal 1965, il segno di un numero intero si rappresenta attraverso il complemento alla base (complemento a due) che ha delle proprietà importanti, ma per comprenderle occorre vedere quali sono state le alternative precedenti.
Il primo modo utilizzato per rappresentare un numero intero con segno è stato quello di attribuire a un bit (probabilmente quello più significativo) il ruolo di indicatore del segno. Per esempio, 000010102 andrebbe interpretato come +1010, mentre 100010102 rappresenterebbe il valore -1010. In questo modo, disponendo di otto cifre binarie, dovendone riservare una per il segno, si potrebbero rappresentare valori da -127 (111111112) a +127 (011111112); inoltre, lo zero potrebbe essere rappresentato indifferentemente come 000000002 o come 10000002.
Il secondo metodo (usato per esempio nel PDP-1) prevede la rappresentazione dei numeri negativi come complemento a uno del valore positivo corrispondente. Il complemento a uno si ottiene invertendo le cifre del numero binario. In questo modo, per esempio, 000010102 rappresenterebbe sempre il valore +1010, mentre 111101012 corrisponderebbe a -1010. Anche in questo caso la prima cifra rappresenta il segno (dove la cifra uno indica un valore negativo), ma il segno si aggiorna automaticamente con la semplice inversione del valore. Utilizzando il complemento a uno per rappresentare i valori negativi, come nel caso precedente, su otto cifre complessive si possono indicare valori da -127 a +127 e lo zero si può rappresentare ancora in due modi differenti: 000000002 o 111111112.
|
Disponendo di una variabile per rappresentare valori interi con segno, considerato che il bit più significativo serve a rappresentare il segno stesso, si dispone di un bit in meno per indicare il valore. Pertanto, se si dispone di n bit, si possono rappresentare valori fino a n-1 bit, ovvero valori fino a 2(n-1)-1. Per i numeri negativi, il calcolo è lo stesso, anche se si considera che si fa riferimento a valori complementati: si può rappresentare fino a -(2(n-1)-1).
|
Il complemento alla base (ovvero il complemento a due) che è invece il metodo attuale per rappresentare i valori interi negativi, ha i vantaggi del metodo del complemento a uno, ma in più ha un solo modo per rappresentare lo zero.
63.3.4
Complemento a due
Attualmente, per rappresentare valori interi con segno (positivo o negativo), si utilizza il metodo del complemento alla base, ovvero del complemento a due, dove il primo bit indica sempre il segno. Il complemento a due si ottiene facilmente calcolando prima il complemento a uno e poi aggiungendo una unità al risultato. Per esempio, se si prende un valore positivo rappresentato in otto cifre binarie come 000101002 (pari a +2010), il complemento a uno è 111010112; aggiungendo una unità si ottiene il complemento a due: 111011002.
Utilizzando questo metodo, per cambiare di segno a un valore è sufficiente calcolarne il complemento a due (esattamente come si farebbe con il metodo del complemento a uno). Lo si verifica facilmente: riprendendo l'esempio già fatto, partendo da -2010 che si rappresenta come 111011002, si calcola prima il complemento a uno, ottenendo così 000100112, quindi si somma una unità e si ottiene 000101002, pari a +2010.
Con il complemento a due, disponendo di n cifre binarie, si possono rappresentare valori da -2(n-1) a +2(n-1)-1 ed esiste un solo modo per rappresentare lo zero: quando tutte le cifre binarie sono pari a zero. Infatti, rimanendo nell'ipotesi di otto cifre binarie, il complemento a uno di 000000002 è 111111112, ma aggiungendo una unità per ottenere il complemento a due si ottiene di nuovo 000000002, perdendo il riporto.
Si osservi che il valore negativo più grande rappresentabile non può essere trasformato in un valore positivo corrispondente, perché si creerebbe un traboccamento. Per esempio, utilizzando sempre otto bit (segno incluso), il valore minimo che possa essere rappresentato è 10000002, pari a -12810, ma se si calcola il complemento a due, si ottiene di nuovo lo stesso valore binario, che però non è valido. Infatti, il valore positivo massimo che si possa rappresentare in questo caso è solo +12710.
|
Figura 63.24. Confronto tra due valori interi con segno.
|
|
Figura 63.25. Valori massimi rappresentabili con soli otto bit.
|
Il meccanismo del complemento a due ha il vantaggio di trasformare la sottrazione in una semplice somma algebrica.
63.3.5
Rappresentazione binaria di numeri in virgola mobile
Una forma diffusa per rappresentare dei valori molto grandi, consiste nell'indicare un numero con dei decimali moltiplicato per un valore costante elevato a un esponente intero. Per esempio, per rappresentare il numero 123 000 000 si potrebbe scrivere 123·106, oppure anche 0,123·109. Lo stesso ragionamento vale anche per valori molti piccoli; per esempio 0,000 000 123 che si potrebbe esprimere come 0,123·10-6.
Per usare una notazione uniforme, si può convenire di indicare il numero che appare prima della moltiplicazione per la costante elevata a una certa potenza come un valore che più si avvicina all'unità, essendo minore o al massimo uguale a uno. Pertanto, per gli esempi già mostrati, si tratterebbe sempre di 0,123·10n.
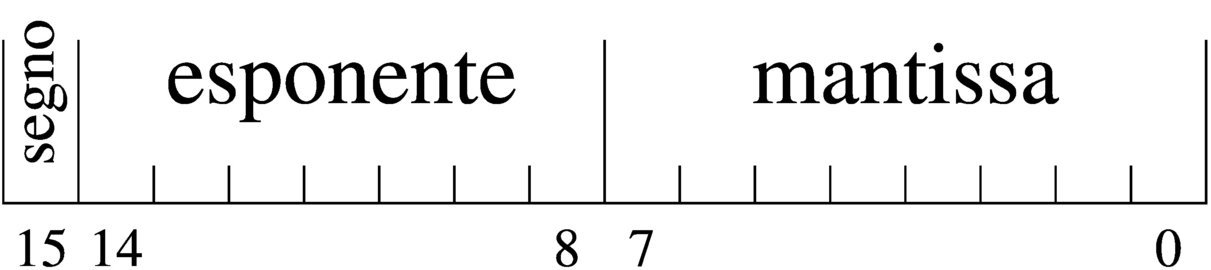
Per rappresentare valori a virgola mobile in modo binario, si usa un sistema simile, dove i bit a disposizione della variabile vengono suddivisi in tre parti: segno, esponente (di una base prestabilita) e mantissa, come nell'esempio che appare nella figura successiva.(2)
|
Figura 63.26. Ipotesi di una variabile a 16 bit per rappresentare dei numeri a virgola mobile.
|
Nella figura si ipotizza la gestione di una variabile a 16 bit per la rappresentazione di valori a virgola mobile. Come si vede dallo schema, il bit più significativo della variabile viene utilizzato per rappresentare il segno del numero; i sette bit successivi si usano per indicare l'esponente (con segno) e gli otto bit finali per la mantissa (senza segno perché indicato nel primo bit), ovvero il valore da moltiplicare per una certa costante elevata all'esponente.
Quello che manca da decidere è come deve essere interpretato il numero della mantissa e qual è il valore della costante da elevare all'esponente indicato. Sempre a titolo di esempio, si conviene che il valore indicato nella mantissa esprima precisamente «0,mantissa» e che la costante da elevare all'esponente indicato sia 16 (ovvero 24), che si traduce in pratica nello spostamento della virgola di quattro cifre binarie alla volta.(3)
|
Figura 63.27. Esempio di rappresentazione del numero 0,051 513 671 875 (211·16-3), secondo le convenzioni stabilite. Si osservi che il valore dell'esponente è negativo ed è così rappresentato come complemento alla base (due) del valore assoluto relativo.
|
Naturalmente, le convenzioni possono essere cambiate: per esempio il segno lo si può incorporare nella mantissa; si può rappresentare l'esponente attraverso un numero al quale deve essere sottratta una costante fissa; si può stabilire un valore diverso della costante da elevare all'esponente; si possono distribuire diversamente gli spazi assegnati all'esponente e alla mantissa.
63.3.6
Rappresentazione in virgola mobile IEEE 754
Per la rappresentazione dei valori in virgola mobile esiste uno standard importante, IEEE 754 (ripreso anche da altri enti di standardizzazione), con il quale si definiscono due formati, per la precisione singola e doppia. Secondo questo standard, un valore in virgola mobile a precisione singola richiede 32 bit, mentre per la precisione doppia sono necessari 64 bit. Per prima cosa si definisce un «numero normalizzato», corrispondente a:(4)
1,significante2 × 2esponente
Di questo si utilizza solo il significante (mantissa) e l'esponente (caratteristica), omettendo il numero uno iniziale. Nella forma prevista dallo standard IEEE 754 si annota separatamente il segno del numero, quindi l'esponente, che però è «polarizzato» (nel senso che al valore dell'esponente originario occorre sommare un certo valore fisso), quindi si mettono le cifre del significante (tutte quelle che possono starci). Si osservi che il significante viene indicato sempre come valore assoluto, pertanto non si applica il complemento per i valori negativi; inoltre, l'esponente viene indicato sommando al valore originale un numero fisso che è costituito da tutti i bit a uno, tranne quello più significativo (quando l'esponente è formato da otto bit, il numero da sommare è 011111112, pari a 12710; quando l'esponente è formato da 11 bit, il numero da sommare è 011111111112, pari a 102310).
|
Figura 63.28. IEEE 754 a precisione singola.
|
|
Figura 63.29. IEEE 754 a precisione doppia.
|
Conviene fare un esempio con la precisione singola: si vuole rappresentare il valore 21,1110. Si procede convertendo separatamente la parte intera e poi quella decimale. Il numero 2110 si converte facilmente in 101012, mentre per la parte decimale occorre fare qualche calcolo in più:
0,11 × 2 = 0,22 → ,02
0,22 × 2 = 0,44 → ,002
0,44 × 2 = 0,88 → ,0002
0,88 × 2 = 1,76 → ,00012
0,76 × 2 = 1,52 → ,000112
0,52 × 2 = 1,04 → ,0001112
0,04 × 2 = 0,08 → ,00011102
0,08 × 2 = 0,16 → ,000111002
0,16 × 2 = 0,32 → ,0001110002
0,32 × 2 = 0,64 → ,00011100002
0,64 × 2 = 1,28 → ,000111000012
0,28 × 2 = 0,56 → ,0001110000102
0,56 × 2 = 1,12 → ,00011100001012
0,12 × 2 = 0,24 → ,000111000010102
0,24 × 2 = 0,48 → ,0001110000101002
0,48 × 2 = 0,96 → ,00011100001010002
0,96 × 2 = 1,92 → ,000111000010100012
0,92 × 2 = 1,84 → ,0001110000101000112
0,84 × 2 = 1,68 → ,00011100001010001112
0,68 × 2 = 1,36 → ,000111000010100011112
0,36 × 2 = 0,72 → ,0001110000101000111102
...
Pertanto, 21,1110 corrisponde approssimativamente a 10101,0001110000101000111102. Per normalizzare il numero occorre spostare la virgola a sinistra e moltiplicare per una potenza di due: 1,01010001110000101000111102 × 24.
A questo punto si prelevano 23 cifre dopo la virgola, ma si richiede un arrotondamento (in questo caso avviene per eccesso), pertanto le cifre che compongono il significante diventano: 010100011100001010010002. L'esponente va sommato al valore costante stabilito: 4+127 = 131. Quindi l'esponente si rappresenta così: 100000112. Trattandosi di un numero positivo, il bit del segno deve essere zero. Ecco il numero in virgola mobile, a precisione singola, espresso secondo la notazione standard (gli spazi aggiunti servono a facilitarne la lettura):
0 10000011 010100011100001010010002
Con questo metodo, un numero a precisione singola può avere un valore assoluto da 12 × 2-126 a 1,1111...2 × 2+127; mentre un numero a precisione doppia può avere un valore assoluto da 12 × 2-1 022 a 1,1111...2 × 2+1 023. Quando si devono rappresentare valori molto bassi, si azzerano i bit dell'esponente e si usa una forma «denormalizzata» di questo tipo per la precisione singola:
0,significante2 × 2-127
Per la precisione doppia:
0,significante2 × 2-1 024
63.3.7
Ordine dei byte(5)
Generalmente si distinguono i microprocessori in base a una caratteristica legata al modo di ordinare i bit di un numero, presi a gruppi di otto. In pratica, di norma la memoria centrale degli elaboratori è organizzata a celle di otto bit (un byte), mentre il microprocessore è in grado di elaborare dati numerici con una quantità di bit maggiore (ma sempre multipli di otto). Nel momento in cui il microprocessore accede alla memoria centrale per leggere o scrivere un valore, lo fa secondo un ordine che dipende dalla sua progettazione.
Supponendo di avere a che fare con il valore 13579BDF16, se il microprocessore lo memorizza secondo la stessa sequenza (ovvero memorizza i byte 1316, 5716, 9B16 e DF16), allora si dice che la sua architettura è big endian; diversamente, se il microprocessore memorizza invertendo la sequenza di byte (quindi DF16, 9B16, 5716 e 1316) si dice che questo lavora in modalità little endian.
Naturalmente, il microprocessore che scrive in memoria un valore secondo una sequenza di byte invertita, quando va a leggerlo dalla memoria si aspetta di trovarlo invertito nello stesso modo.
|
Sia chiaro che, all'interno di ogni byte, l'ordine dei bit non viene modificato. Inoltre, nel momento in cui si pensa a un'elaborazione all'interno del microprocessore, con dati contenuti nei suoi registri, non ha importanza conoscere qual è l'ordine dei byte.
|
63.4
Calcoli con i valori binari rappresentati nella forma usata negli elaboratori
Una volta chiarito il modo in cui si rappresentano comunemente i valori numerici elaborati da un microprocessore, in particolare per ciò che riguarda i valori negativi con il complemento a due, occorre conoscere in che modo si trattano o si possono trattare questi dati (indipendentemente dall'ordine dei byte usato).
Questi concetti tornano utili nella programmazione in linguaggio macchina o nei linguaggi assemblatori equivalenti, ma servono anche per linguaggi evoluti che conservano una rappresentazione dei valori conforme all'architettura dell'elaboratore.
63.4.1
Modifica della quantità di cifre di un numero binario intero
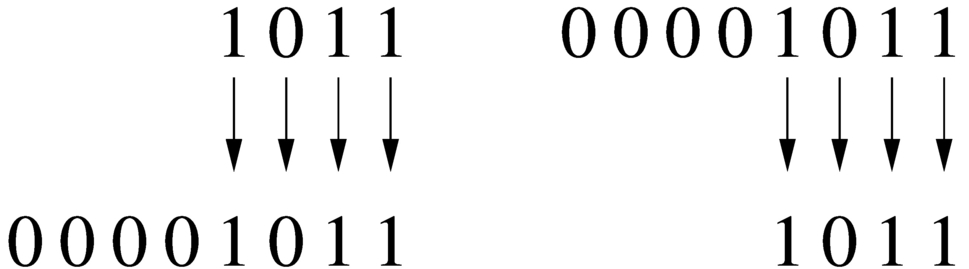
Un numero intero senza segno, espresso con una certa quantità di cifre, può essere trasformato in una quantità di cifre maggiore, aggiungendo degli zeri nella parte più significativa. Per esempio, il numero 01012 può essere trasformato in 000001012 senza cambiarne il valore. Nello stesso modo, si può fare una copia di un valore in un contenitore più piccolo, perdendo le cifre più significative, purché queste siano a zero, altrimenti il valore risultante sarebbe alterato.
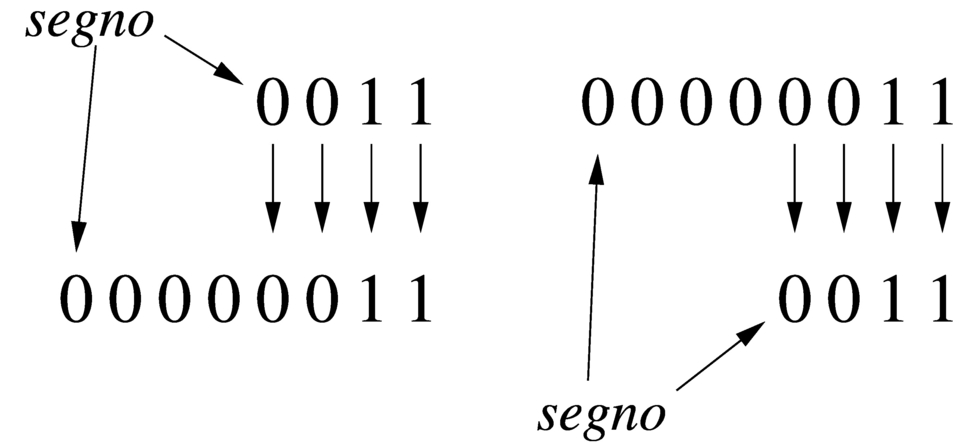
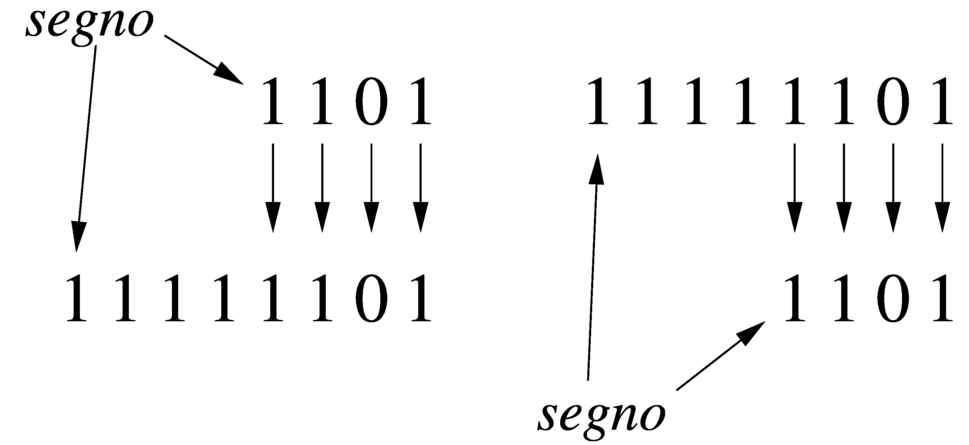
Quando si ha a che fare con valori interi con segno, nel caso di valori positivi, l'estensione e la riduzione funzionano come per i valori senza segno, con la differenza che nella riduzione di cifre, la prima deve ancora rappresentare un segno positivo. Se invece si ha a che fare con valori negativi, l'aumento di cifre richiede l'aggiunta di cifre a uno nella parte più significativa, mentre la riduzione comporta l'eliminazione di cifre a uno nella parte più significativa, con il vincolo di mantenere inalterato il segno.
|
Figura 63.30. Aumento e riduzione delle cifre di un numero intero senza segno.
|
|
Figura 63.31. Aumento e riduzione delle cifre di un numero intero positivo.
|
|
Figura 63.32. Aumento e riduzione delle cifre di un numero intero negativo.
|
63.4.2
Sommatorie con i valori interi con segno
Vengono proposti alcuni esempi che servono a dimostrare le situazioni che si presentano quando si sommano valori con segno, ricordando che i valori negativi sono rappresentati come complemento alla base del valore assoluto corrispondente.
|
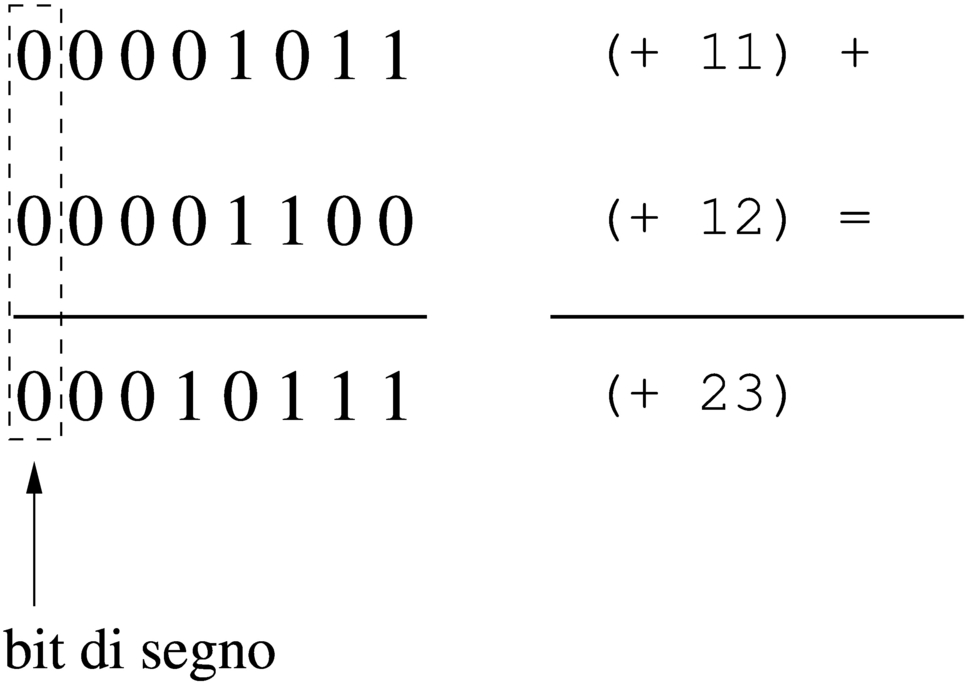
Figura 63.33. Somma di due valori positivi che genera un risultato valido.
|
|
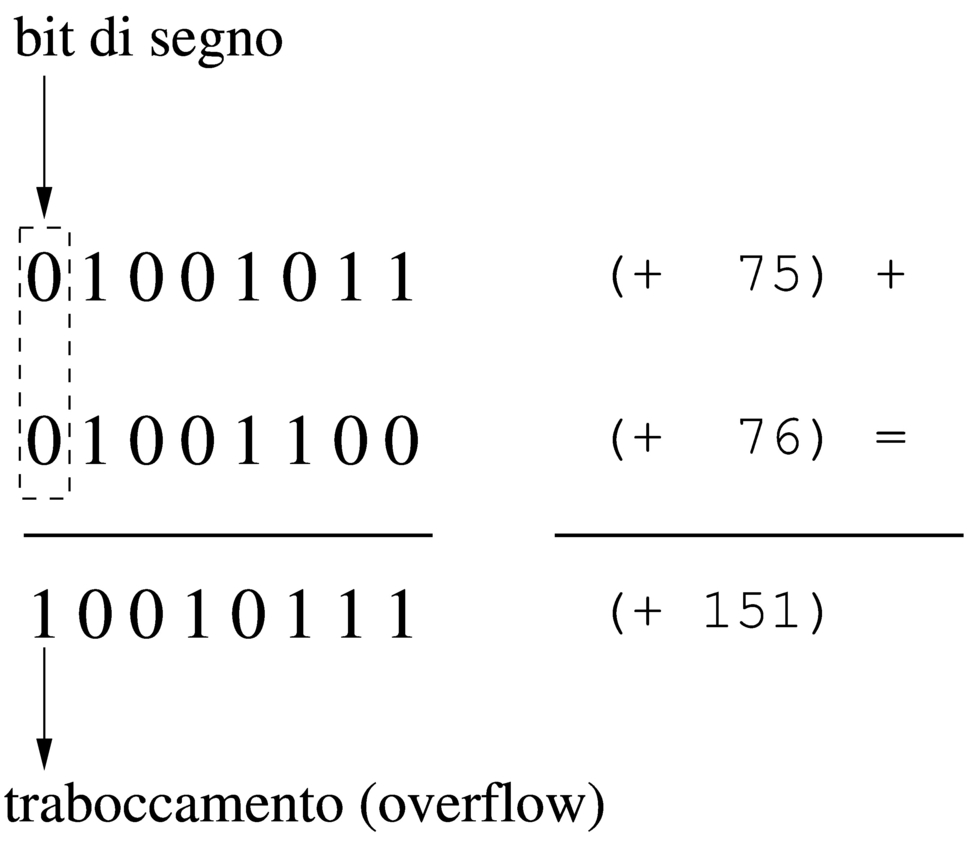
Figura 63.34. Somma di due valori positivi, dove il risultato apparentemente negativo indica la presenza di un traboccamento.
|
|
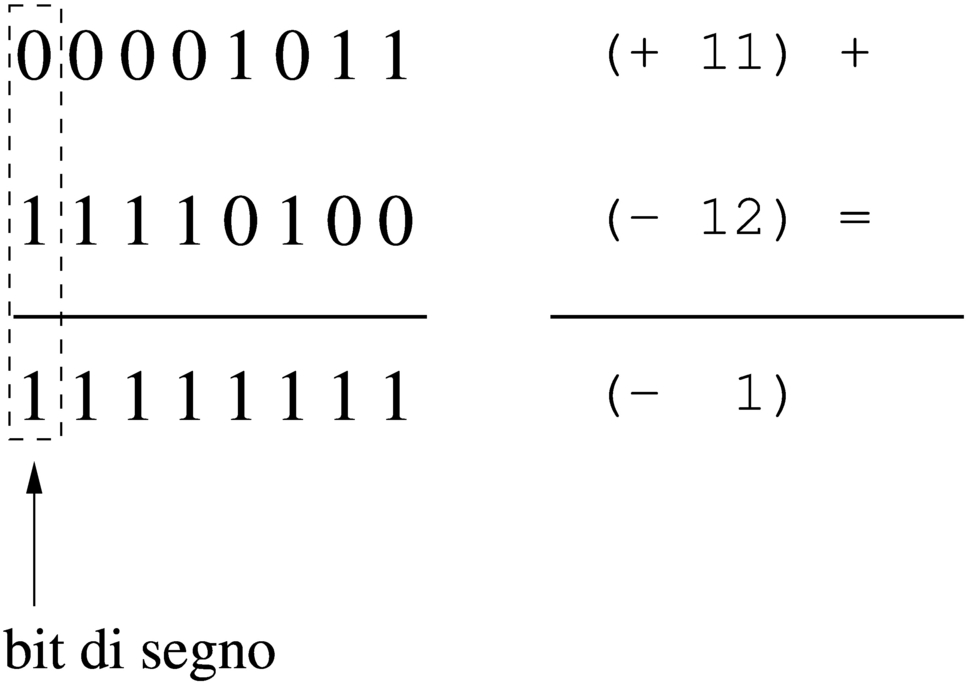
Figura 63.35. Somma di un valore positivo e di un valore negativo: il risultato è sempre valido.
|
|
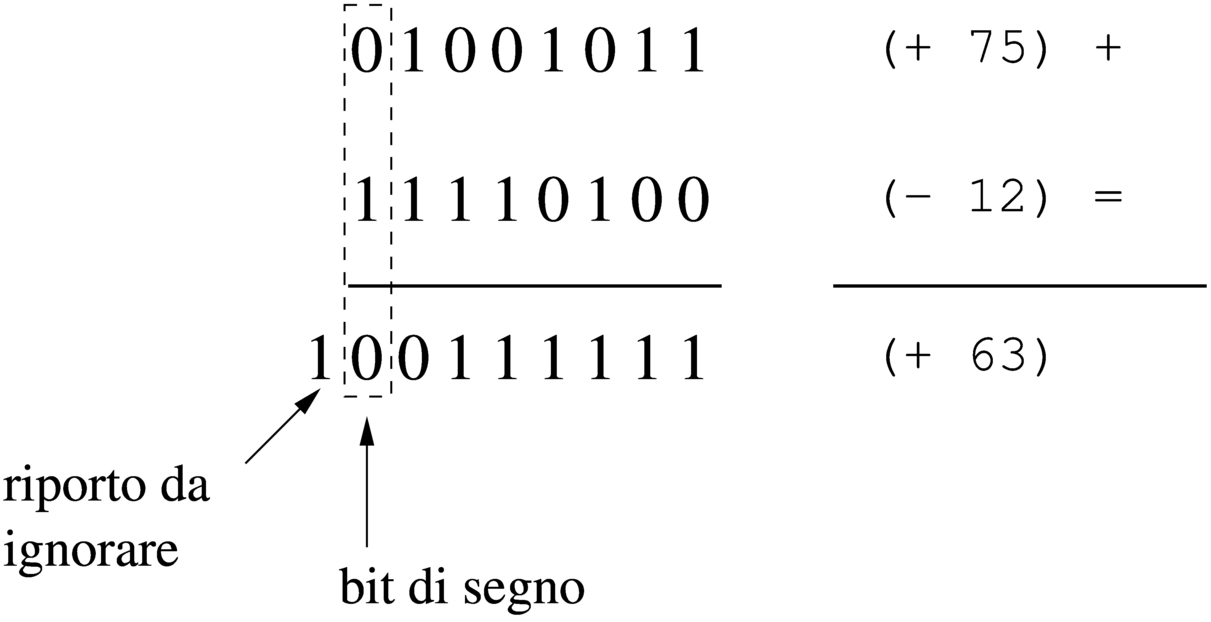
Figura 63.36. Somma di un valore positivo e di un valore negativo: in tal caso il risultato è sempre valido e se si manifesta un riporto, come in questo caso, va ignorato semplicemente.
|
|
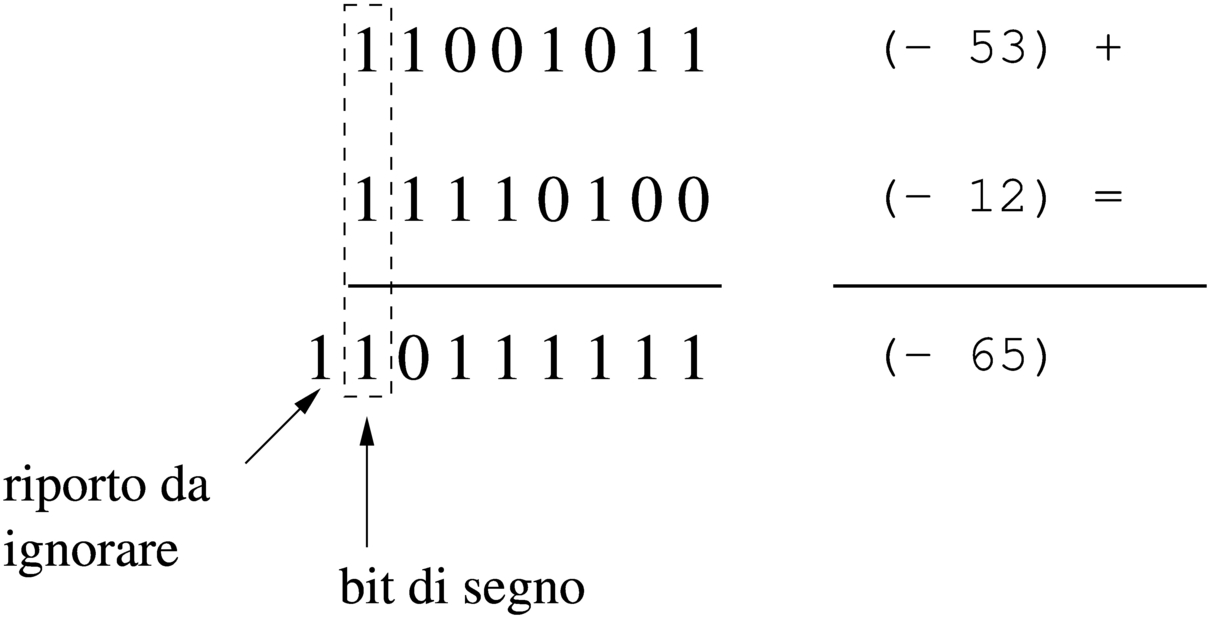
Figura 63.37. Somma di due valori negativi che produce un segno coerente e un riporto da ignorare.
|
|
Figura 63.38. Somma di due valori negativi che genera un traboccamento, evidenziato da un risultato con un segno incoerente.
|
Dagli esempi mostrati si comprende facilmente che la somma di due valori con segno va fatta ignorando il riporto, perché quello che conta è che il segno risultante sia coerente: se si sommano due valori positivi, perché il risultato sia valido deve essere positivo; se si somma un valore positivo con uno negativo il risultato è sempre valido; se si sommano due valori negativi, perché il risultato sia valido deve rimanere negativo.
63.4.3
Somme e sottrazioni con i valori interi senza segno
La somma di due numeri interi senza segno avviene normalmente, senza dare un valore particolare al bit più significativo, pertanto, se si genera un riporto, il risultato non è valido (salva la possibilità di considerarlo assieme al riporto). Se invece si vuole eseguire una sottrazione, il valore da sottrarre va «invertito», con il complemento a due, ma sempre evitando di dare un significato particolare al bit più significativo. Il valore «normale» e quello «invertito» vanno sommati come al solito, ma se il risultato non genera un riporto, allora è sbagliato, in quanto il sottraendo è più grande del minuendo.
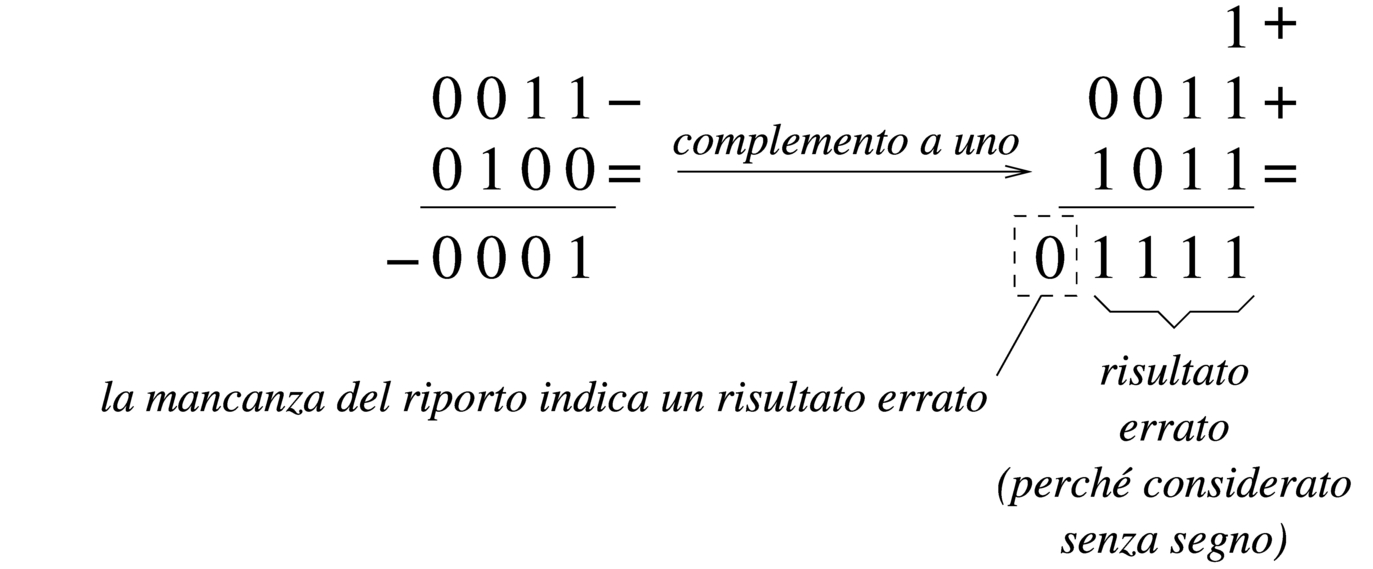
Per comprendere come funziona la sottrazione, si consideri di volere eseguire un'operazione molto semplice: 1-1. Il minuendo (il primo valore) sia espresso come 000000012; il sottraendo (il secondo valore) che sarebbe uguale, va trasformato attraverso il complemento a due, diventando così pari a 111111112. A questo punto si sommano algebricamente i due valori e si ottiene 000000002 con riporto di uno. Il riporto di uno dà la garanzia che il risultato è corretto. Volendo provare a sottrarre un valore più grande, si vede che il riporto non viene ottenuto: 1-2. In questo caso il minuendo si esprime come nell'esempio precedente, mentre il sottraendo è 000000102 che si trasforma nel complemento a due 111111102. Se si sommano i due valori si ottiene semplicemente 111111112, senza riporto, ma questo valore che va inteso senza segno è evidentemente errato.
|
Figura 63.39. Sottrazione tra due numeri interi senza segno, dove il sottraendo ha un valore assoluto minore di quello del minuendo: la presenza del riporto conferma la validità del risultato.
|
|
Figura 63.40. Sottrazione tra due numeri interi senza segno, dove il sottraendo ha un valore assoluto maggiore di quello del minuendo: l'assenza di un riporto indica un risultato errato della sottrazione.
|
Sulla base della spiegazione data, c'è però un problema, dovuto al fatto che il complemento a due di un valore a zero dà sempre zero: se si fa la sottrazione con il complemento, il risultato è comunque corretto, ma non si ottiene un riporto.
|
Figura 63.41. Sottrazione con sottraendo a zero: non si ottiene riporto, ma il risultato è corretto ugualmente.
|
Per correggere questo problema, il complemento a due del numero da sottrarre, va eseguito in due fasi: prima si calcola il complemento a uno, poi si somma il minuendo al sottraendo complementato, aggiungendo una unità ulteriore. Le figure successive ripetono gli esempi già mostrati, attuando questo procedimento differente.
|
Figura 63.42. Il complemento a due viene calcolato in due fasi: prima si calcola il complemento a uno, poi si sommano il minuendo e il sottraendo invertito, più una unità.
|
|
Figura 63.44. Sottrazione con sottraendo a zero: calcolando il complemento a due attraverso il complemento a uno, si ottiene un riporto coerente.
|
63.4.4
Somme e sottrazioni in fasi successive
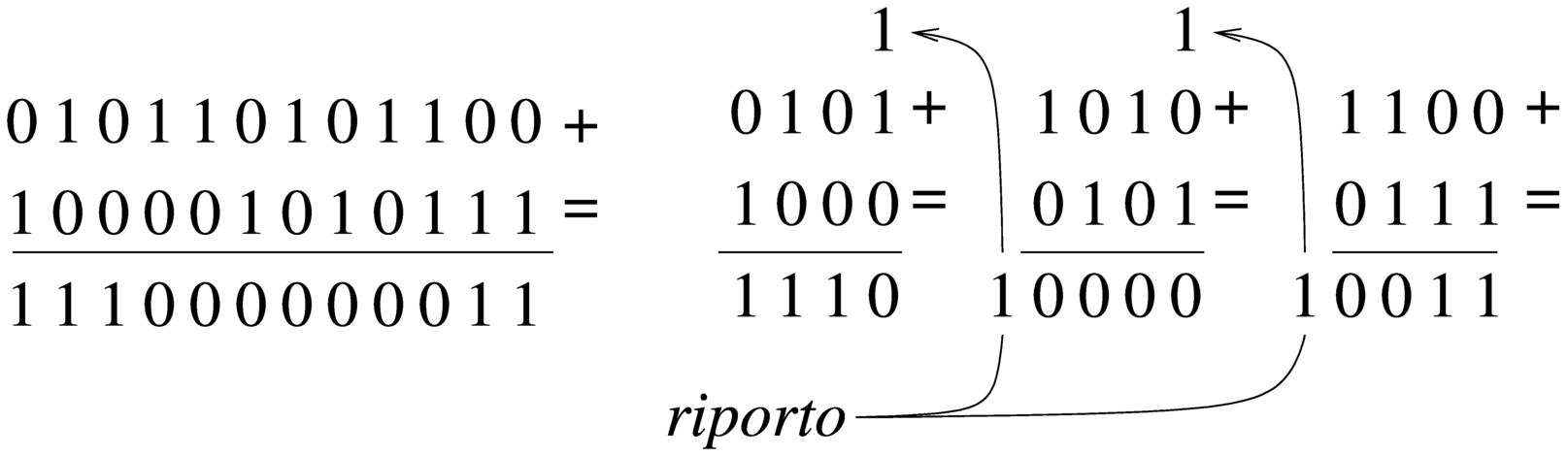
Quando si possono eseguire somme e sottrazioni solo con una quantità limitata di cifre, mentre si vuole eseguire un calcolo con numeri più grandi della capacità consentita, si possono suddividere le operazioni in diverse fasi. La somma tra due numeri interi è molto semplice, perché ci si limita a tenere conto del riporto ottenuto nelle fasi precedenti. Per esempio, dovendo sommare 0101 1010 11002 a 1000 0101 01112 e potendo operare solo a gruppi di quattro bit per volta: si parte dal primo gruppo di bit meno significativo, 11002 e 01112, si sommano i due valori e si ottiene 00112 con riporto di uno; si prosegue sommando 10102 con 01012 aggiungendo il riporto e ottenendo 00002 con riporto di uno; si conclude sommando 01012 e 10002, aggiungendo il riporto della somma precedente e si ottiene così 11102. Quindi, il risultato è 1110 0000 00112.
|
Figura 63.45. Somma per fasi successive, tenendo conto del riporto.
|
Nella sottrazione tra numeri senza segno, il sottraendo va trasformato secondo il complemento a due, quindi si esegue la somma e si considera che ci deve essere un riporto, altrimenti significa che il sottraendo è maggiore del minuendo. Quando si deve eseguire la sottrazione a gruppi di cifre più piccoli di quelli che richiede il valore per essere rappresentato, si può procedere in modo simile a quello che si usa con la somma, con la differenza che «l'assenza del riporto» indica la richiesta di prendere a prestito una cifra.
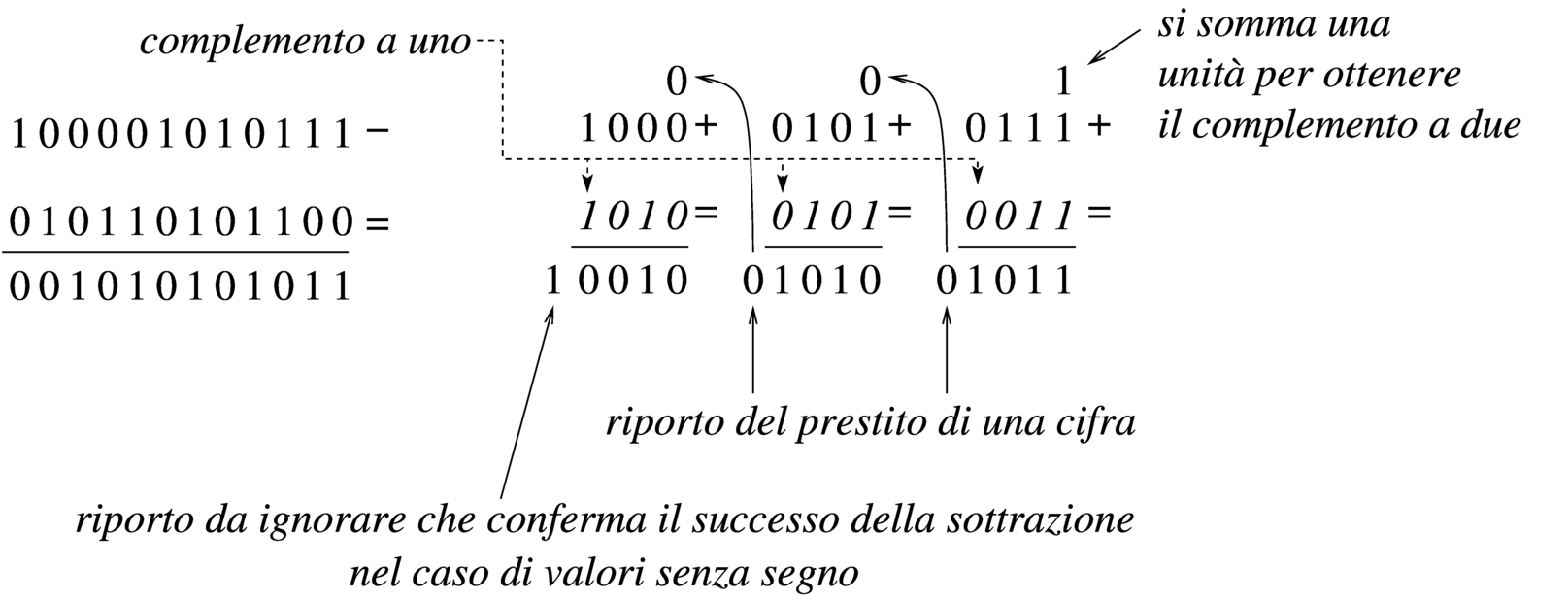
Per comprendere il procedimento è meglio partire da un esempio. In questo caso si utilizzano i valori già visti, ma invece di sommarli si vuole eseguire la sottrazione. Per la precisione, si intende prendere 1000 0101 01112 come minuendo e 0101 1010 11002 come sottraendo. Anche in questo caso si suppone di poter eseguire le operazioni solo a gruppi di quattro bit. Si esegue il complemento a due dei tre gruppetti di quattro bit del sottraendo, in modo indipendente, ottenendo: 10112, 01102, 01002. A questo punto si eseguono le somme, a partire dal gruppo meno significativo. La prima somma, 01112 + 01002, dà 10112, senza riporto, pertanto occorre prendere a prestito una cifra dal gruppo successivo: ciò significa che va eseguita la somma del gruppo successivo, sottraendo una unità dal risultato: 01012 + 01102 - 00012 = 10102. Anche per il secondo gruppo non si ottiene il riporto della somma, così, anche dal terzo gruppo di bit occorre prendere a prestito una cifra: 10002 + 10112 - 00012 = 00102. L'ultima volta la somma genera il riporto (da ignorare) che conferma la correttezza del risultato complessivo, ovvero che la sottrazione è avvenuta con successo.
Va però ricordato il problema legato allo zero, il cui complemento a due dà sempre zero. Se si cambiano i valori dell'esempio, lasciando come minuendo quello precedente, 1000 0101 01112, ma modificando il sottraendo in modo da avere le ultime quattro cifre a zero, 0101 1010 00002, il procedimento descritto non funziona più. Infatti, il complemento a due di 00002 rimane 00002 e se si somma questo a 01112 si ottiene lo stesso valore, ma senza riporti. In questo caso, nonostante l'assenza del riporto, il gruppo dei quattro bit successivi, del sottraendo, va trasformato con il complemento a due, senza togliere l'unità che sarebbe prevista secondo l'esempio precedente. In pratica, per poter eseguire la sottrazione per fasi successive, occorre definire un concetto diverso: il prestito (borrow) che non deve scattare quando si sottrae un valore pari a zero.
Se il complemento a due viene ottenuto passando per il complemento a uno, con l'aggiunta di una cifra, si può spiegare in modo più semplice il procedimento della sottrazione per fasi successive: invece di calcolare il complemento a due dei vari tronconi, si calcola semplicemente il complemento a uno e al gruppo meno significativo si aggiunge una unità per ottenere lì l'equivalente di un complemento a due. Successivamente, il riporto delle somme eseguite va aggiunto al gruppo adiacente più significativo, come si farebbe con la somma: se la sottrazione del gruppo precedente non ha bisogno del prestito di una cifra, si ottiene l'aggiunta una unità al gruppo successivo.
|
Figura 63.46. Sottrazione per fasi successive, tenendo conto del prestito delle cifre.
|
|
Figura 63.47. Verifica del procedimento anche in presenza di un sottraendo a zero.
|
La sottrazione per fasi successive funziona anche con valori che, complessivamente, hanno un segno. L'unica differenza sta nel modo di valutare il risultato complessivo: l'ultimo gruppo di cifre a essere considerato (quello più significativo) è quello che contiene il segno ed è il segno del risultato che deve essere coerente, per stabilire se ciò che si è ottenuto è valido. Pertanto, nel caso di valori con segno, il riporto finale si ignora, esattamente come si fa quando la sottrazione avviene in una fase sola, mentre l'esistenza o meno del traboccamento deriva dal confronto della cifra più significativa: se la sottrazione, dopo la trasformazione in somma con il complemento, implica la somma valori con lo stesso segno, il risultato deve ancora avere quel segno, altrimenti c'è il traboccamento.
Se si volessero considerare gli ultimi due esempi come la sottrazione di valori con segno, il minuendo si intenderebbe un valore negativo, mentre il sottraendo sarebbe un valore positivo. Attraverso il complemento si passa alla somma di due valori negativi, ma dal momento che si ottiene un risultato con segno positivo, ciò manifesta un traboccamento, ovvero un risultato errato, perché non contenibile nello spazio disponibile.
63.4.5
Indicatori
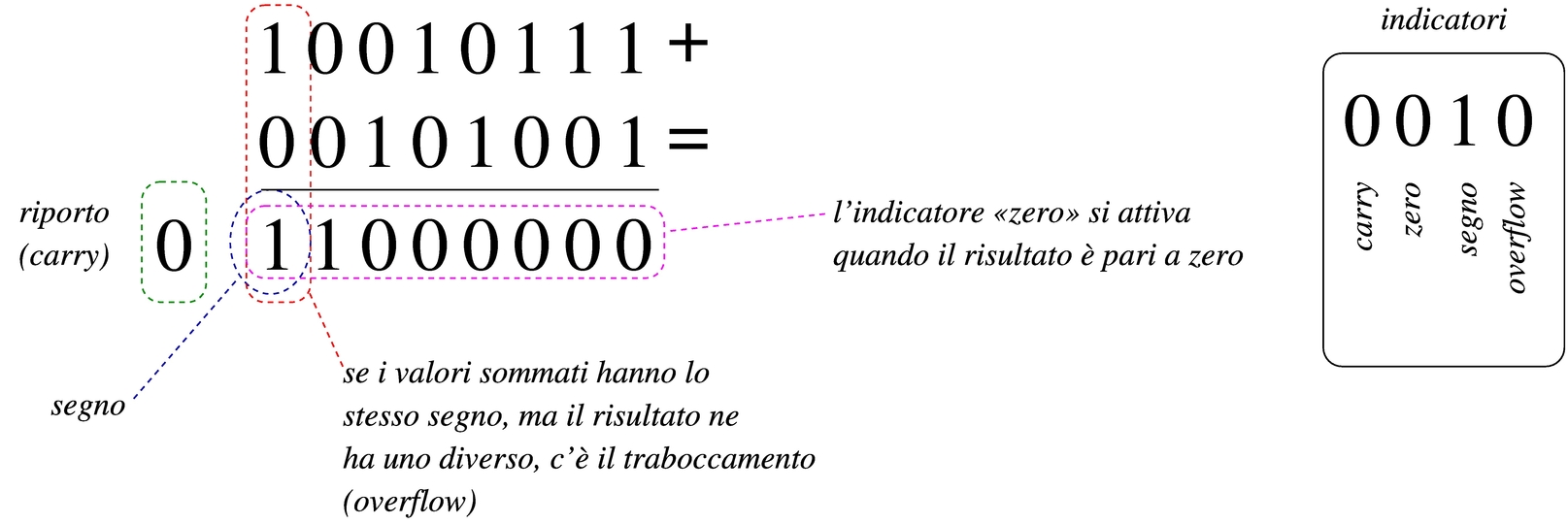
Quando si esegue un calcolo con un microprocessore, oltre al risultato puro e semplice è necessario annotare altre informazioni sull'esito dell'operazione stessa. Come già descritto, una somma può dare luogo a un traboccamento o a un riporto, così come una sottrazione può richiedere un prestito di una cifra. Queste e altre informazioni, che non possono essere incorporate nel risultato di un calcolo, finiscono all'interno di indicatori (flag), ovvero di bit singoli, ognuno con un proprio significato preciso. Le figure successive dimostrano il funzionamento degli indicatori più comuni.
|
Figura 63.48. Somma di interi: se i numeri sono da intendersi senza segno, il risultato non è completo in quanto si genera un riporto; se i numeri sono da intendersi con segno, in tal caso sono negativi, ma la loro somma produce un traboccamento.
|
|
Figura 63.49. Somma di interi: se i numeri sono da intendersi senza segno, il risultato non è completo in quanto si genera un riporto; se i numeri sono da intendersi con segno, in tal caso hanno segni diversi tra di loro e questo impedisce che si crei un traboccamento, inoltre il risultato è zero e si attiva l'indicatore relativo.
|
|
Figura 63.50. Somma di interi: se i numeri sono da intendersi senza segno, il risultato è completo in quanto non si genera un riporto; se i numeri sono da intendersi con segno, in tal caso hanno segni diversi tra di loro e questo impedisce che si crei un traboccamento, inoltre il risultato è negativo e questo attiva l'indicatore di segno.
|
Come già descritto in altre sezioni, le sottrazioni vanno eseguite calcolando prima il complemento a uno del sottraendo e poi aggiungendo una unità ulteriore. In questo modo, ciò che nella somma rappresenterebbe un riporto, qui va invertito per segnalare la richiesta di un prestito (borrow).
|
Figura 63.51. Sottrazione di interi: se i numeri sono da intendersi senza segno, il risultato è completo in quanto non si genera la richiesta di prestito di una cifra; se i numeri sono da intendersi con segno, si tratta di valori negativi, ma la somma genera un cambiamento di segno, pertanto si attiva l'indicatore di traboccamento.
|
|
Figura 63.52. Sottrazione di interi: qui viene sottratto zero da un valore. Utilizzando il meccanismo del complemento a uno, aggiungendo una unità alla somma, si evita che scatti la richiesta di prestito, come è logico che sia. In questo caso, dato che il risultato è negativo, si attiva l'indicatore di segno.
|
63.5
Scorrimenti, rotazioni, operazioni logiche
Le operazioni più semplici che si possono compiere con un microprocessore sono quelle che riguardano la logica booleana e lo scorrimento dei bit. Proprio per la loro semplicità è importante conoscere alcune applicazioni interessanti di questi procedimenti elaborativi.
63.5.1
Scorrimento logico
Lo scorrimento «logico» consiste nel fare scalare le cifre di un numero binario, verso sinistra (verso la parte più significativa) o verso destra (verso la parte meno significativa). Nell'eseguire questo scorrimento, da un lato si perde una cifra, mentre dall'altro si acquista uno zero.
|
Figura 63.53. Scorrimento logico a sinistra, perdendo le cifre più significative e scorrimento logico a destra, perdendo le cifre meno significative.
|
Lo scorrimento di una posizione verso sinistra corrisponde alla moltiplicazione del valore per due, mentre lo scorrimento a destra corrisponde a una divisione intera per due; scorrimenti di n posizioni rappresentano moltiplicazioni e divisioni per 2n. Le cifre che si perdono nello scorrimento a sinistra si possono considerare come il riporto della moltiplicazione, mentre le cifre che si perdono nello scorrimento a destra sono il resto della divisione.
63.5.2
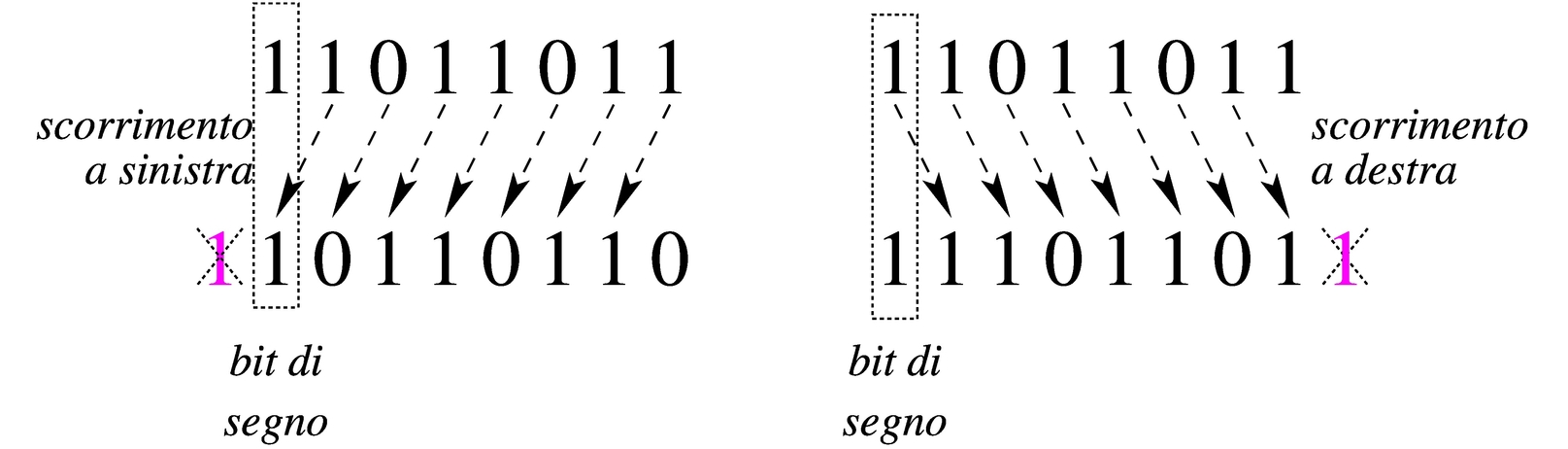
Scorrimento aritmetico
Il tipo di scorrimento descritto nella sezione precedente, se utilizzato per eseguire moltiplicazioni e divisioni, va bene solo per valori senza segno. Se si intende fare lo scorrimento di un valore con segno, occorre distinguere due casi: lo scorrimento a sinistra è valido se il risultato non cambia di segno; lo scorrimento a destra implica il mantenimento del bit che rappresenta il segno e l'aggiunta di cifre uguali a quella che rappresenta il segno stesso.
|
Figura 63.54. Scorrimento aritmetico a sinistra e a destra, di un valore negativo.
|
63.5.3
Scorrimento e indicatori
Tenendo conto che gli scorrimenti si eseguono sempre per una sola posizione alla volta e che rappresentano una moltiplicazione o una divisione per due, tornano utili gli stessi indicatori descritti a proposito di somme e sottrazioni. Come già accennato, il riporto viene usato per segnalare la cifra che viene perduta (sia per lo scorrimento verso sinistra, sia per quello verso destra), mentre l'indicatore di traboccamento (overflow) serve a segnalare che il risultato cambia di segno.
Lo scorrimento aritmetico verso sinistra avviene nello stesso modo di quello «logico». Nel caso il valore che viene fatto scorrere sia considerato privo di segno, il risultato della moltiplicazione per due è valido se non si presenta un riporto; se invece il valore ha un segno, il risultato è «corretto» se il segno non è cambiato.
|
Figura 63.55. Scorrimento a sinistra. Nel lato sinistro si vede che il risultato non è valido se si tratta di un valore senza segno, in quanto si presenta un riporto, mentre sarebbe valido se fosse un valore con segno, perché questo non cambia. A destra, invece, si vede un valore che se è da intendere senza segno, dà un risultato corretto, mentre se ha il segno, il risultato non è più valido perché il segno si inverte (overflow).
|
Lo scorrimento verso destra avviene in modo diverso se il valore va inteso con segno o senza segno, perché se si presta attenzione al segno si usa lo scorrimento aritmetico che inserisce a sinistra cifre uguali al segno precedente. Pertanto, nello scorrimento a destra si considera solo il resto, che finisce in pratica nello stesso indicatore del riporto.
|
Figura 63.56. Nel lato sinistro si vede uno scorrimento «logico» che produce un resto, mentre in quello destro si vede uno scorrimento aritmetico che, in questo caso, non produce alcun resto.
|
63.5.4
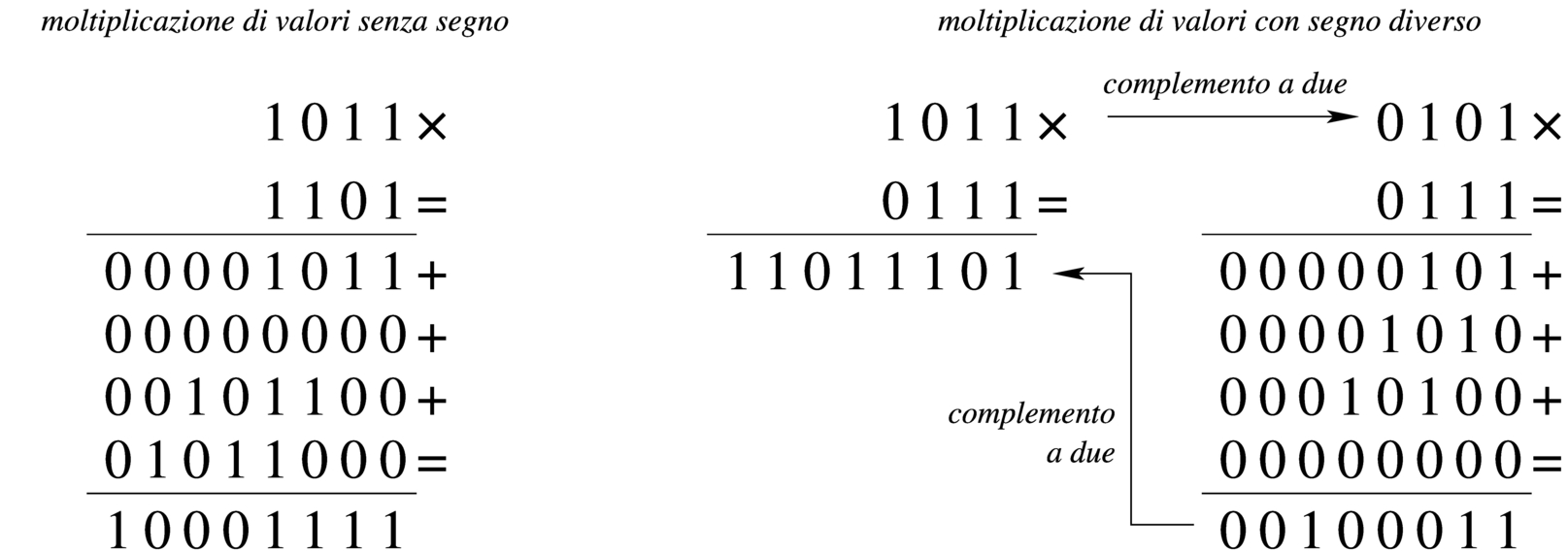
Moltiplicazione
La moltiplicazione si ottiene attraverso diverse fasi di scorrimento e somma di un valore, dove però il risultato richiede un numero doppio di cifre rispetto a quelle usate per il moltiplicando e il moltiplicatore. Il procedimento di moltiplicazione deve avvenire sempre con valori senza segno. Se i valori si intendono con segno, quando sono negativi occorre farne prima il complemento a due, in modo da portarli a valori positivi, quindi occorre decidere se il risultato va preso così come viene o se va invertito a sua volta con il complemento a due: se i valori moltiplicati hanno segno diverso tra loro, il risultato deve essere trasformato con il complemento a due per renderlo negativo, altrimenti il risultato è sempre positivo.
|
Figura 63.57. Moltiplicazione.
|
63.5.5
Divisione
La divisione si ottiene attraverso diverse fasi di scorrimento di un valore, che di volta in volta viene sottratto al dividendo, ma solo se la sottrazione è possibile effettivamente. Il procedimento di divisione deve avvenire sempre con valori senza segno. Se i valori si intendono con segno, quando sono negativi occorre farne prima il complemento a due, in modo da portarli a valori positivi, quindi occorre decidere se il risultato va preso così come viene o se va invertito a sua volta con il complemento a due: se dividendo e divisore hanno segni diversi tra loro, il risultato deve essere trasformato con il complemento a due per renderlo negativo, altrimenti il risultato è sempre positivo.
|
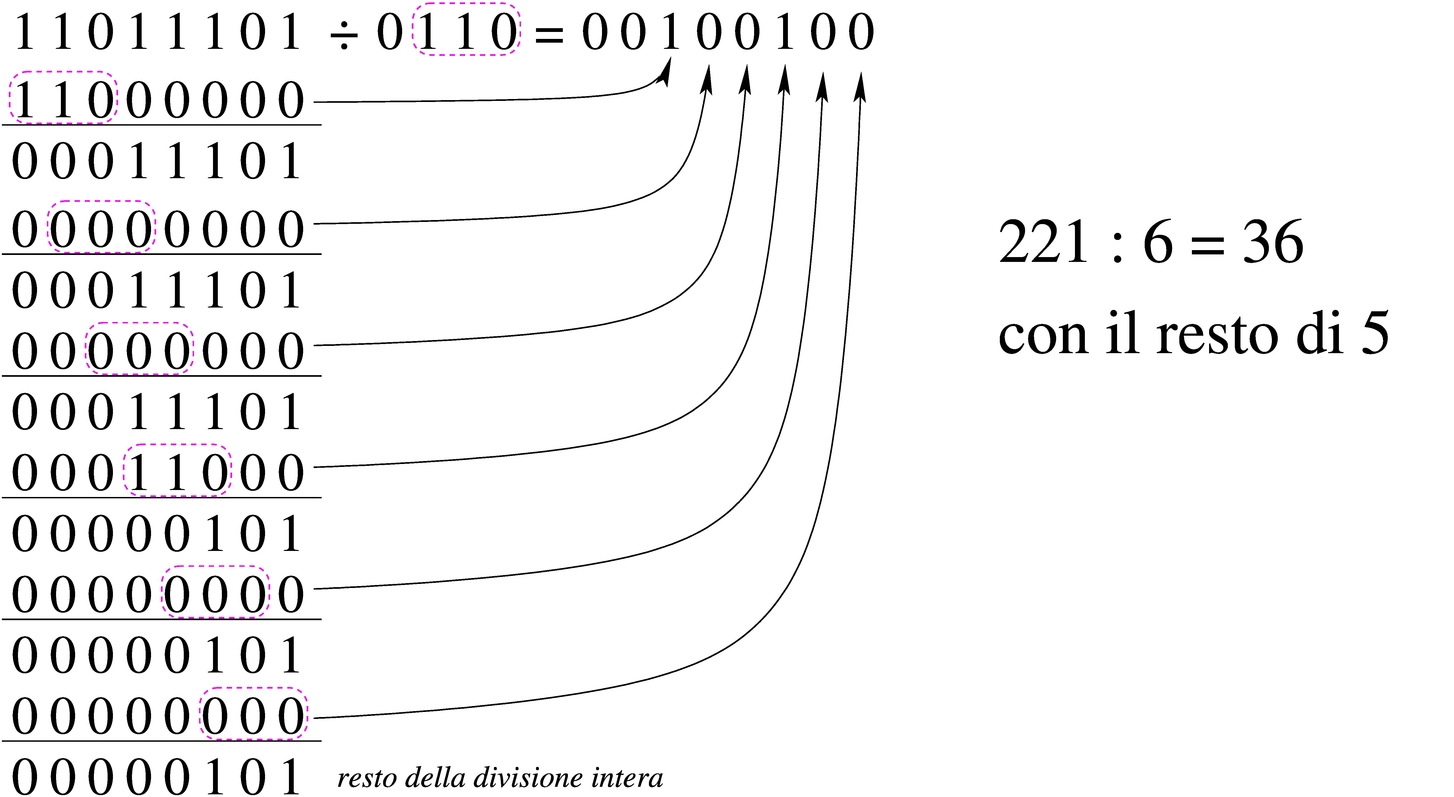
Figura 63.58. Divisione: i valori sono intesi senza segno.
|
63.5.6
Rotazione
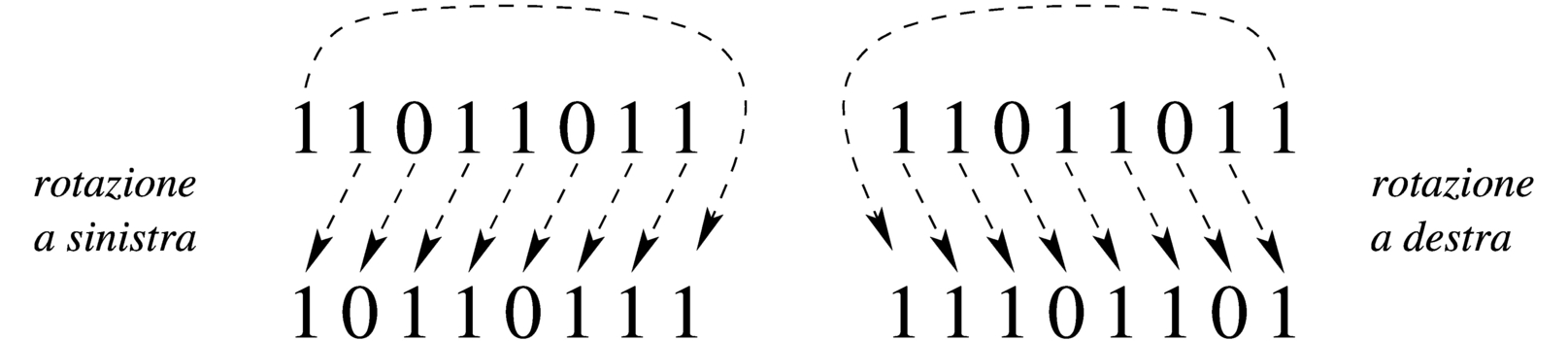
La rotazione è uno scorrimento dove le cifre che si perdono da una parte rientrano dall'altra. Esistono due tipi di rotazione; uno «normale» e l'altro che include nella rotazione il bit del riporto. Dal momento che la rotazione non si presta per i calcoli matematici, di solito non viene considerato il segno.
|
Figura 63.59. Rotazione normale.
|
|
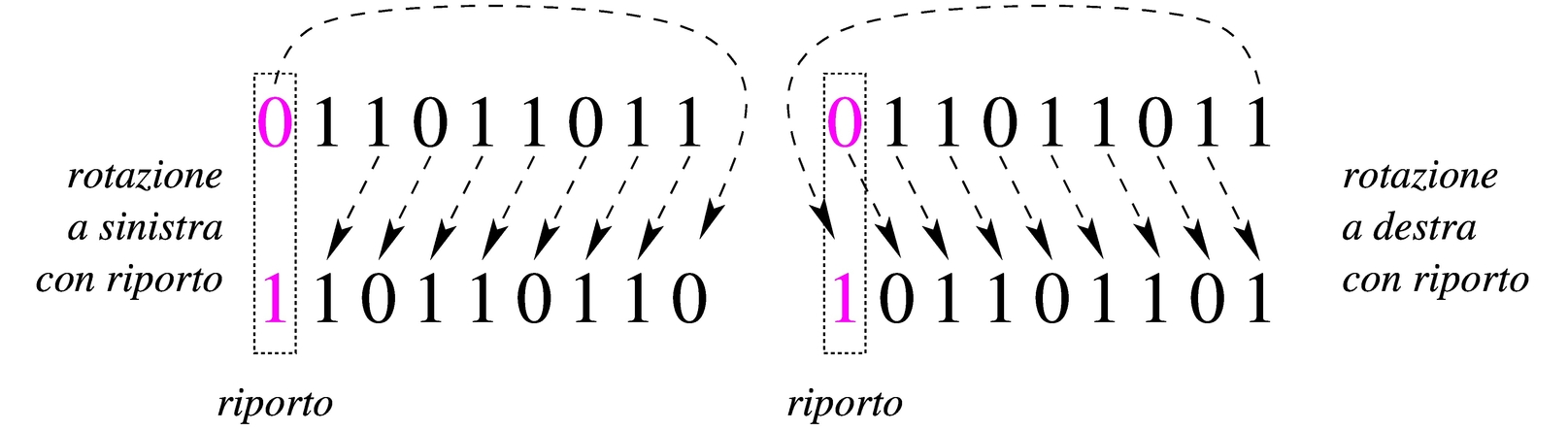
Figura 63.60. Rotazione con riporto.
|
63.5.7
Rotazione e indicatori
Le rotazioni non sono riconducibili a operazioni matematiche, ma si usa ugualmente l'indicatore del riporto per conservare la cifra persa; inoltre, l'indicatore di traboccamento può servire per annotare un'ipotesi di cambiamento di segno.
|
Figura 63.61. Rotazione normale. La cifra che fuoriesce da un lato e rientra dall'altro, rimane annotata nell'indicatore di riporto; nel caso dell'esempio di rotazione a destra, l'indicatore di traboccamento segnala che la cifra più significativa è diversa rispetto alla fase precedente.
|
|
Figura 63.62. Rotazione con riporto. La cifra che fuoriesce da un lato entra nel riporto, mentre dall'altro lato entra la cifra conservata nel riporto precedente; nel caso dell'esempio di rotazione a destra, l'indicatore di traboccamento segnala che la cifra più significativa è diversa rispetto alla fase precedente.
|
63.5.8
Operatori logici
Gli operatori logici si possono applicare anche a valori composti da più cifre binarie.
È importante osservare che l'operatore NOT esegue in pratica il complemento a uno di un valore.
Capita spesso di trovare in un sorgente scritto in un linguaggio assemblatore un'istruzione che assegna a un registro il risultato dell'operatore XOR su se stesso. Ciò si fa, evidentemente, per azzerarne il contenuto, quando, probabilmente, l'assegnamento esplicito di un valore a un registro richiede una frazione di tempo maggiore per la sua esecuzione.
|
Figura 63.65. XOR per azzerare i valori.
|
63.5.9
Intervenire su bit singoli
Quando si lavora con valori binari composti da una quantità prestabilita di cifre, per intervenire singolarmente o comunque solo parzialmente sulle stesse occorre predisporre delle maschere da abbinare poi con un operatore logico appropriato. Segue la descrizione di alcuni esempi.
-
Si vuole attivare il quarto bit (contando a partire dalla cifra meno significativa) nella variabile x.
x := x OR 810
-
Si vuole disattivare il quarto bit (contando a partire dalla cifra meno significativa) nella variabile x.
x := x AND (NOT 810)
-
Si vuole invertire il quarto bit (contando a partire dalla cifra meno significativa) nella variabile x.
x := x XOR 810
-
Si vuole dividere un valore per otto (che è una potenza di due, ovvero 23), calcolando il quoziente intero e il resto. Per farlo occorre far scorrere il valore verso destra, di tre posizioni. Tenendo conto che le cifre che vengono espulse sono quelle che rappresentano il resto, questo lo si può ottenere con una maschera pari a sette (23 - 1), abbinata con l'operatore AND.
63.5.10
Somme e sottrazioni abbinate agli operatori logici
Esiste una proprietà interessante della sottrazione, quando viene abbinata all'operatore logico AND. Come si vede nella figura successiva, quando si riduce un valore di una unità, quella che prima era la cifra a uno meno significativa passa a zero, mentre le cifre precedenti passano a uno. Così facendo, se si abbinano i due valori (quello originale e quello ridotto di una unità) con l'operatore AND, si ottiene un nuovo valore in cui, semplicemente, la cifra meno significativa a uno passa a zero:
Per converso, se si incrementa di una unità un valore e poi si abbinata l'operatore logico OR (tra il valore originale e quello incrementato di una unità), si ottiene di portare a uno la cifra meno significativa che prima era a zero:
63.6
Confronti attraverso la sottrazione
Il confronto tra due valori avviene provando a sottrarne uno dall'altro. In un microprocessore, l'esito di una sottrazione, come mostrato dagli indicatori comuni, consente di confrontare i valori originali.
63.6.1
Confronto di valori senza segno
Se si esegue una sottrazione e si attiva l'indicatore del risultato zero, senza la presenza di una richiesta del prestito di una cifra, i valori sono uguali; se il valore ottenuto è diverso da zero e non c'è alcuna richiesta di prestito, vuol dire che il sottraendo ha un valore inferiore al minuendo; negli altri casi, il sottraendo ha un valore maggiore del minuendo.
|
Figura 63.72. Confronto di valori senza segno.
|
63.6.2
Confronto di valori con segno
Il confronto tra valori con segno avviene in modo meno intuitivo di quello che invece lo ignora. Qui non si considera l'indicatore del prestito di una cifra, mentre vanno considerati al suo posto gli indicatori di segno e di traboccamento, che possono essere uguali o meno tra di loro. Pertanto: se il risultato della sottrazione dà zero, i valori confrontati sono uguali; se il risultato della sottrazione è diverso da zero, se gli indicatori di segno e di traboccamento sono uguali, vuol dire che il sottraendo è inferiore del minuendo; diversamente il sottraendo è superiore al minuendo.
|
Figura 63.73. Confronto di valori con segno.
|
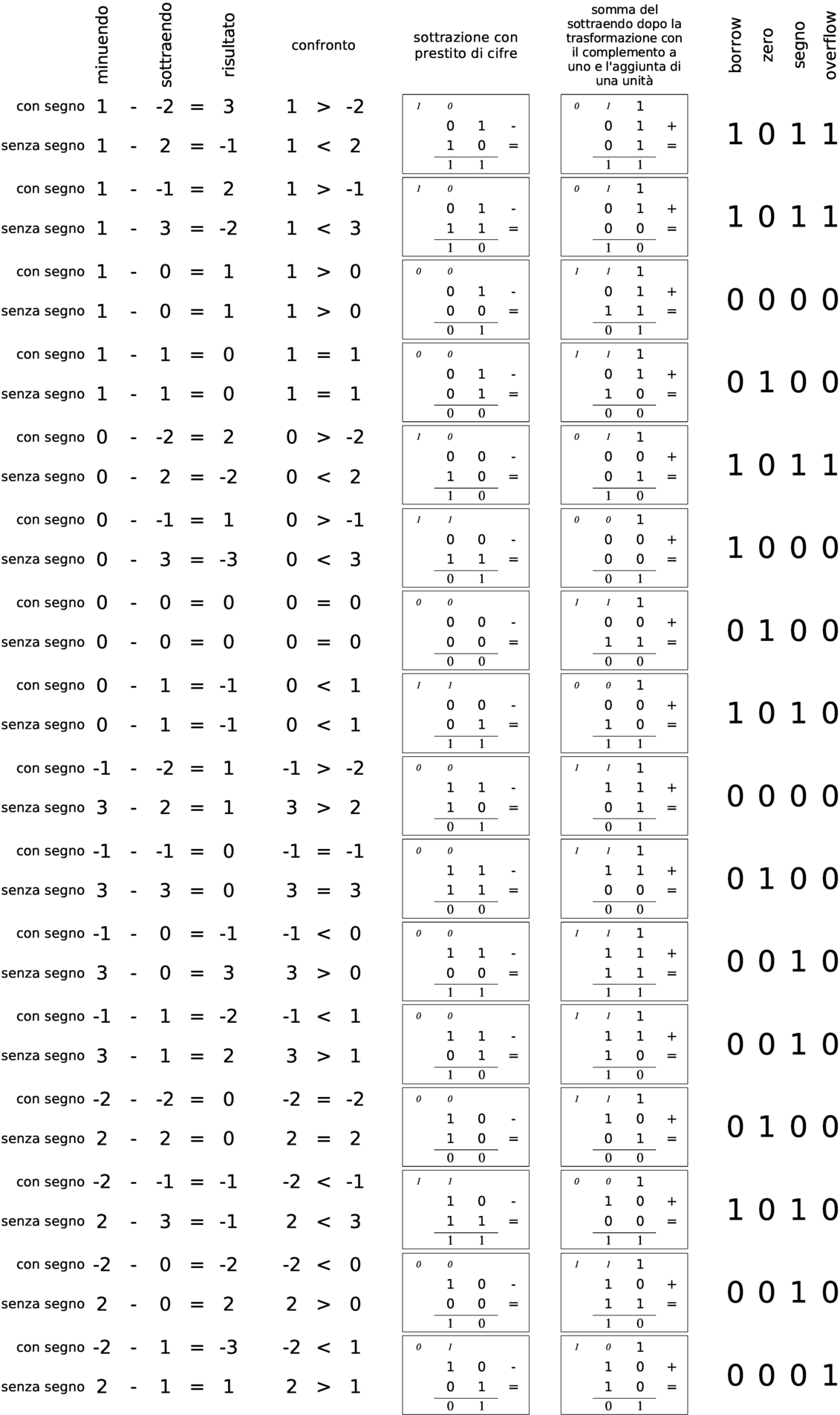
Dal momento che il meccanismo del confronto di valori con segno può essere difficile da comprendere con pochi esempi, si aggiunge un prospetto con i confronti fra tutti i valori che si possono rappresentare con due soli bit, sia senza segno, sia con segno. Nel prospetto viene mostrata la sottrazione e l'addizione dopo l'inversione del sottraendo, inoltre sono annotati tutti i riporti e i prestiti parziali.
|
Figura 63.74. Verifica di tutti i casi di confronto per valori a due bit.
|
63.7
Riferimenti
-
Jonathan Bartlett, Programming from the ground up, 2003, http://savannah.nongnu.org/projects/pgubook/
-
Paul A. Carter, PC Assembly Language, 2006, http://www.drpaulcarter.com/pcasm/
-
Wikipedia, Addressing mode, http://en.wikipedia.org/wiki/Addressing_mode
-
Mario Italiani, Giuseppe Serazzi, Elementi di informatica, ETAS libri, 1973, ISBN 8845303632
-
Sandro Petrizzelli, Appunti di elettronica digitale, http://users.libero.it/sandry/Digitale_01.pdf
-
Tony R. Kuphaldt, Lessons In Electric Circuits, http://www.faqs.org/docs/electric/
-
Wikipedia, Sistema numerico binario
http://it.wikipedia.org/wiki/Sistema_numerico_binario
-
Wikipedia, IEEE 754, http://it.wikipedia.org/wiki/IEEE_754
1) Questa sezione riprende e in parte ripete, per maggiore chiarezza, un concetto già presentato nella sezione 63.1.8.
2) Nel contesto riferito alla definizione di un numero in virgola mobile, si possono usare indifferentemente i termini mantissa o significante, così come sono indifferenti i termini caratteristica o esponente.
3) Si osservi che lo standard IEEE 754 utilizza una «mantissa normalizzata» che indica la frazione di valore tra uno e due: «1,mantissa.
4) Considerato che si tratta di un numero da esprimere in base due, il valore che viene moltiplicato per la potenza di due è un numero che va da uno a due.
5) Per completezza, questa sezione riprende un concetto già descritto nella sezione 63.1.6.
«a2» 2013.11.11 --- Copyright © Daniele Giacomini -- appunti2@gmail.com http://informaticalibera.net