successivo
precedente
inizio
fine
indice generale
aiuto
indice analitico
volume
parte
TXT
HTML
PDF
pdf
gdoc
P4
Costruzione di un'unità aritmetico-logica
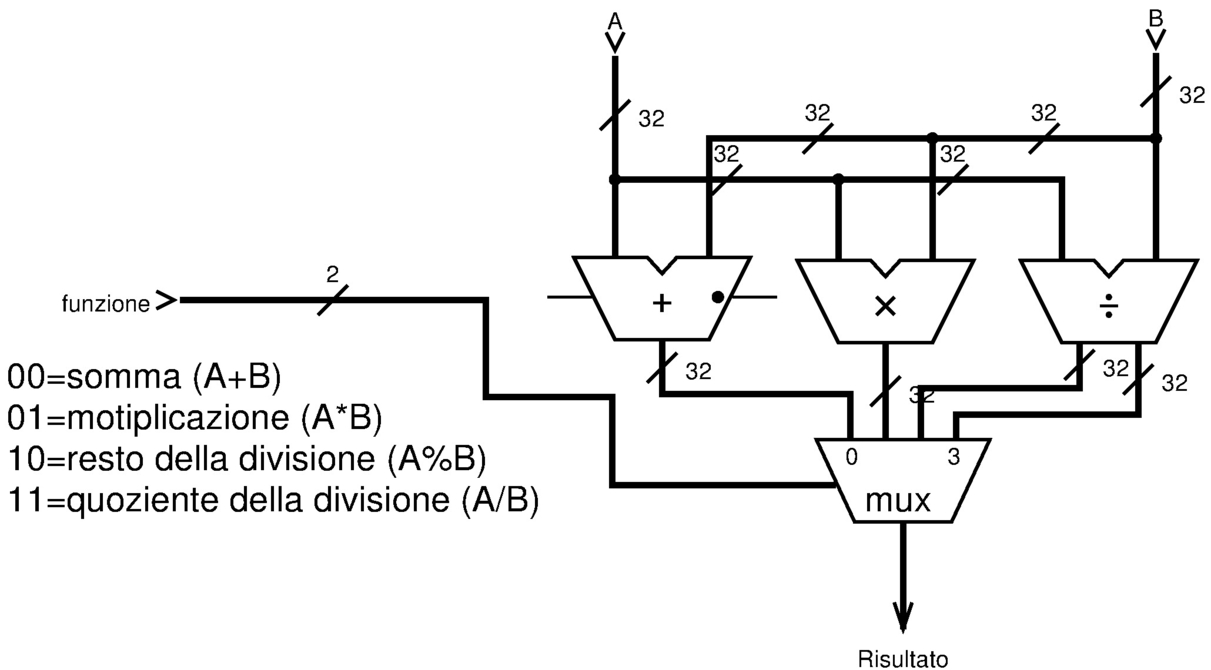
L'unità aritmetico-logica, nota come ALU (arithmetic-logic unit), è un circuito combinatorio che racchiude le funzionalità di calcolo principali di un CPU. Complessivamente si tratta dell'unione di più circuiti combinatori, ognuno dei quali compie un solo tipo o pochi tipi di calcoli; tale complesso si ottiene attraverso l'uso opportuno di multiplatori per selezionare il risultato a cui si è interessati.
|
Figura u127.1. Schema esemplificativo di come si possono connettere assieme più componenti per formare una sola ALU: ogni componente riceve una copia dei valori in ingresso, ma l'uscita viene selezionata da un multiplatore, attraverso un codice che rappresenta la funzione da richiedere alla ALU.
|
Negli esempi, dove possibile, si suddivide il lavoro in moduli da 8 cifre binarie; inoltre, le varie componenti vengono realizzate in modo che possano operare con ranghi differenti di bit: 8, 16, 24 e 32.
Indicatori
Quando opportuno, devono essere fornite informazioni aggiuntive sui risultati dei calcoli, cosa che si fa normalmente attraverso degli indicatori, costituiti in pratica da delle uscite aggiuntive. Gli indicatori più comuni sono: riporto, zero, segno e traboccamento.
| Denominazione | Sigla comune | Descrizione |
| zero | Z | Indica che il risultato dell'operazione è pari a zero. |
| segno negativo | N | Indica che, nel risultato, la cifra più significativa è pari a uno, per cui, se la rappresentazione numerica tiene conto del segno, si tratta di un numero negativo. |
riporto
carry | C | Indica che il risultato complessivo dovrebbe avere una cifra in più rispetto a quanto ottenuto, il quale è così troncato della sua cifra più significativa. |
traboccamento
overflow | O | Si manifesta quando il risultato non è valido perché risulta troncato nella parte più significativa, o perché risulta di segno diverso rispetto a quello che dovrebbe avere. Nella somma lo si determina confrontando gli ultimi due riporti e trovando che sono differenti. |
|
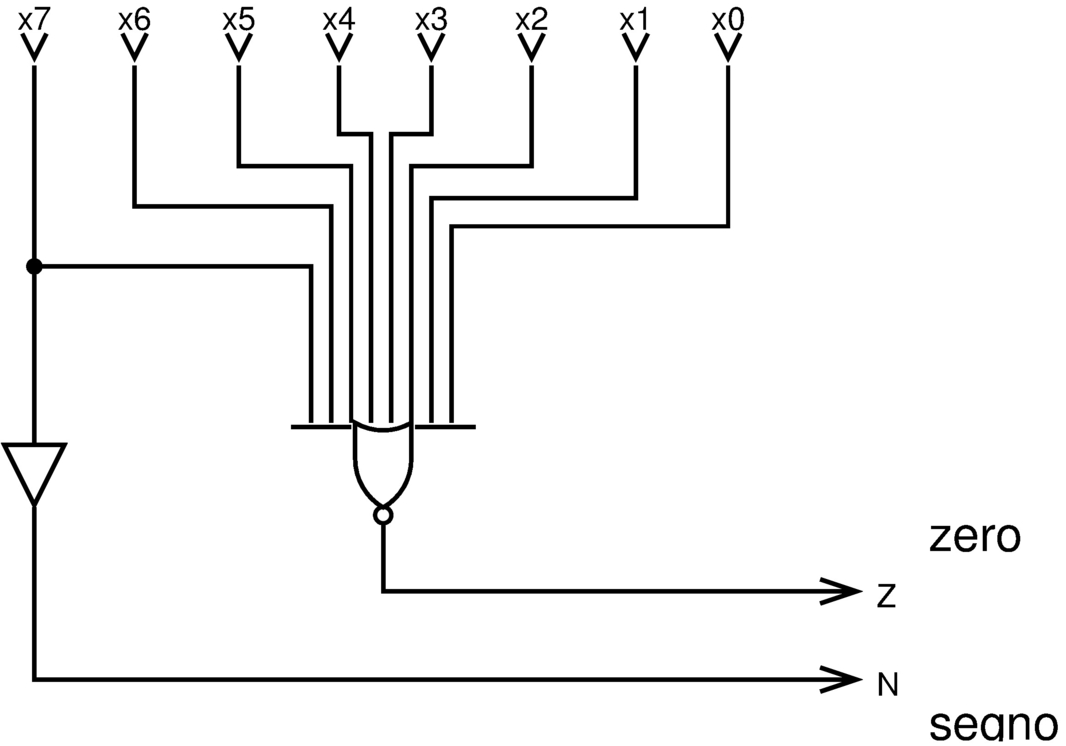
La verifica del risultato pari a zero può essere fatta poco prima dell'uscita dell'ALU, con l'ausilio di una porta NOR, la quale produce un risultato solo quando nessun ingresso è attivo; allo stesso modo, si determina facilmente il segno del risultato (ammesso che il contesto consideri la presenza di un segno), controllando il valore del bit più significativo.
|
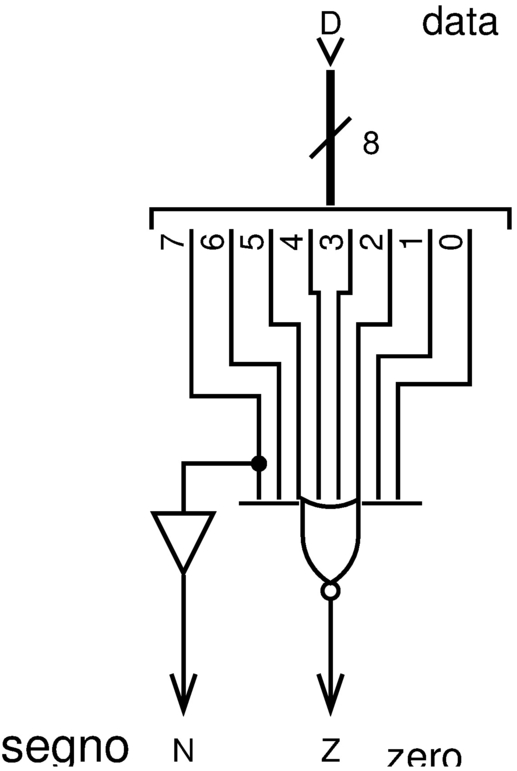
Figura u127.3. Modulo zn8: controllo del risultato pari a zero e della presenza eventuale di un segno. A destra appare lo stesso circuito in modo compatto, dove gli otto ingressi sono raccolti opportunamente.
|
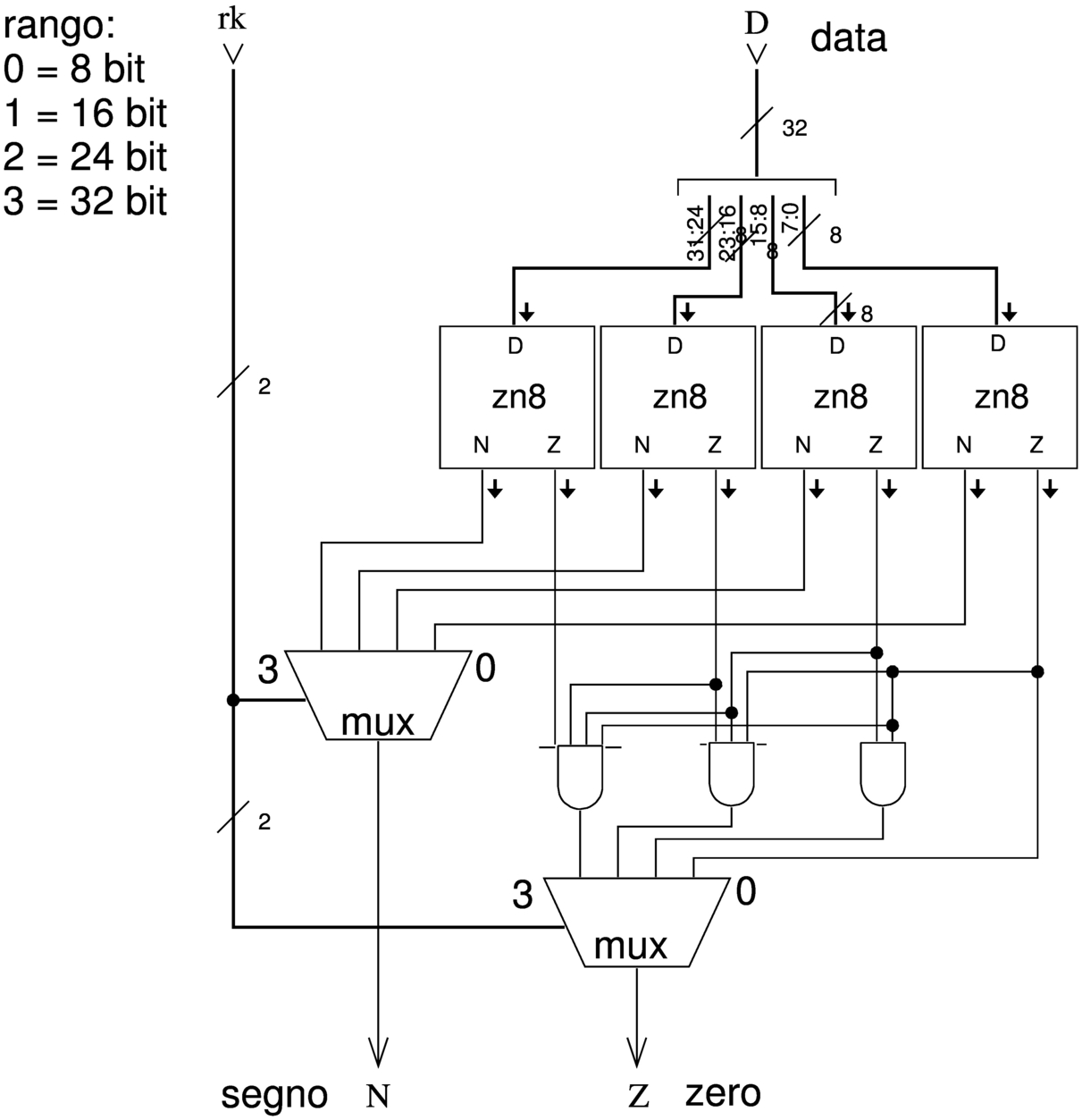
Volendo gestire, a seconda dei casi, interi con rango diverso, si può utilizzare quanto già visto nella figura precedente, in forma di modulo, costruendo un sistema un po' più complesso.
|
Figura u127.4. Modulo zn32: valutazione degli indicatore «zero» e «segno», per interi da 8 a 32 bit. L'ingresso rk (rank) consente di stabilire il rango: si va da zero che rappresenta solo 8 bit, fino a 3 che richiede un rango di 32 bit. Il modulo zn8 è descritto nella figura u127.3.
|
Troncamento di un valore in base al rango
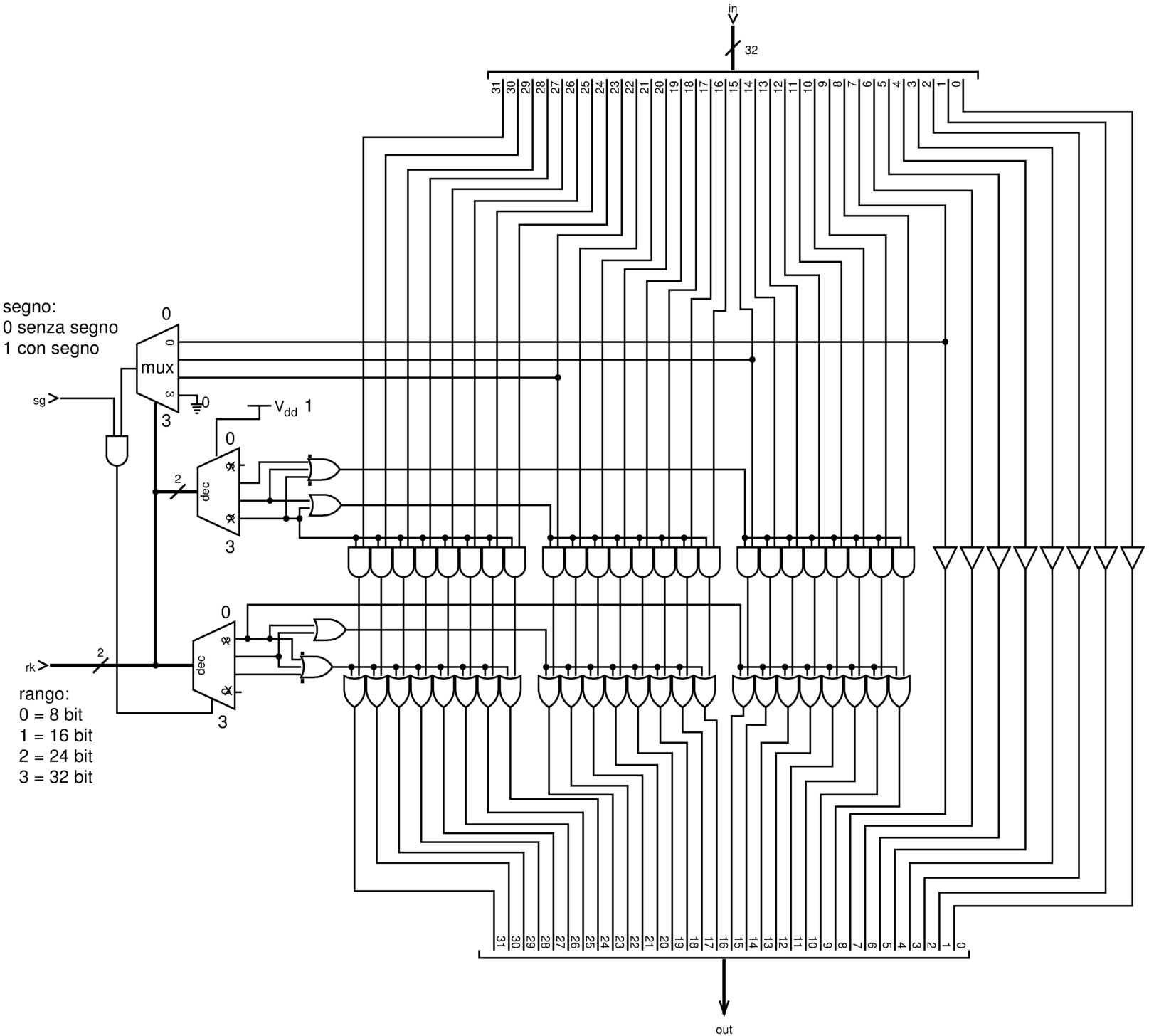
I moduli che vengono presentati nelle sezioni successive, consentono di operare su valori a 32 bit, con la possibilità di limitare l'intervento a ranghi inferiori (ma sempre multipli di otto). I risultati che si ottengono sono validi solo nell'ambito del rango selezionato, ma ci possono essere dei contenuti ulteriori, da ignorare, nei bit più significativi oltre al rango voluto. Il modulo successivo, consente di filtrare opportunamente ciò che è al di fuori del rango desiderato, con la possibilità di estendere il segno, in modo da non creare confusione, o comunque per ridurre la possibilità di errori.
|
Figura u127.5. Modulo rk: filtro dei bit al di fuori del rango selezionato, tenendo conto del segno se il valore in ingresso è da intendersi con segno.
|
Inversione di segno
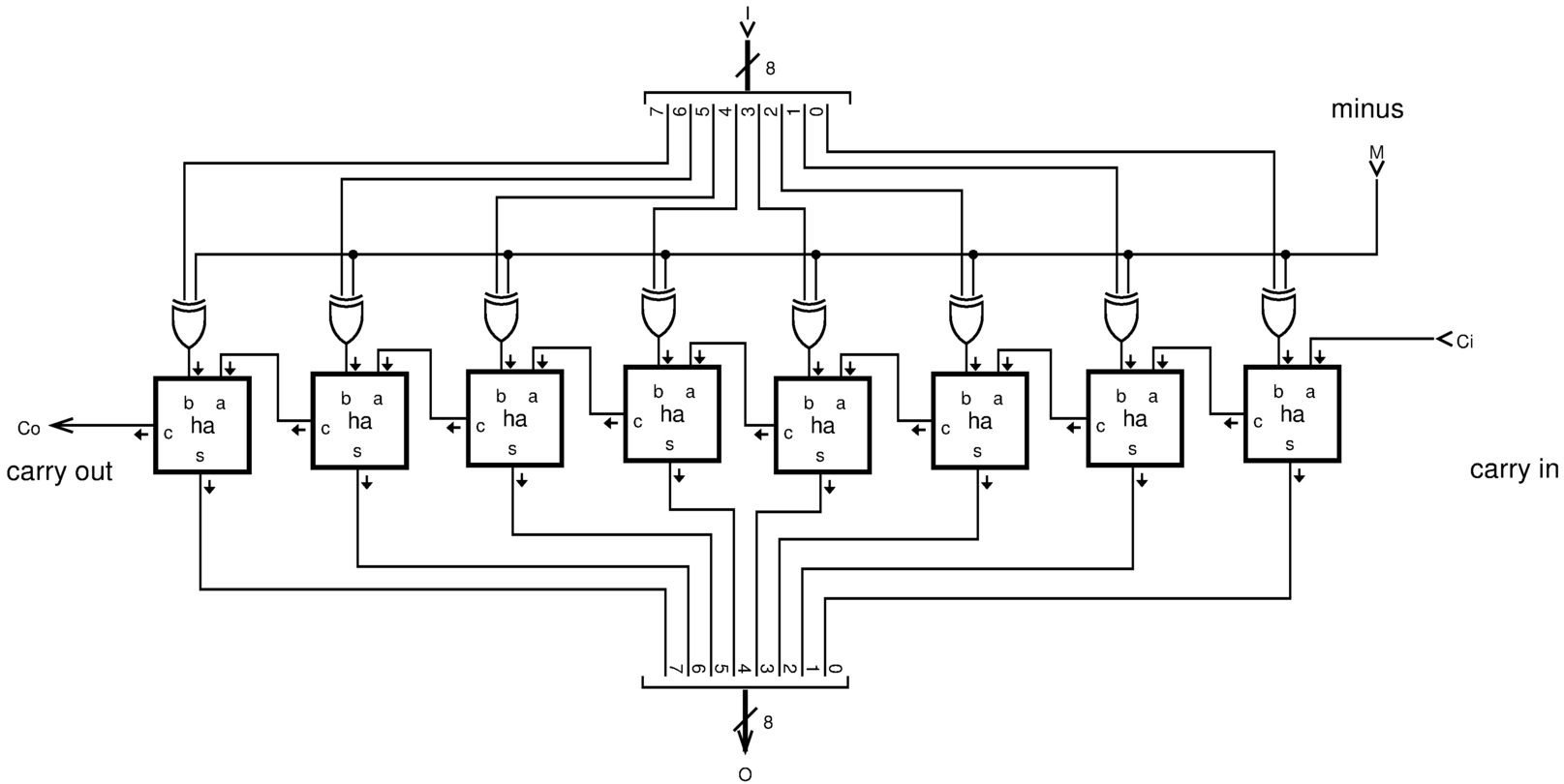
Per la moltiplicazione e la divisione, si rende necessario un modulo in grado di invertire il segno di un numero binario. Il modulo minus8 interviene su 8 bit e serve per realizzare moduli di rango maggiore.
|
Figura u127.6. Modulo minus8: inverte il segno di un numero a 8 bit se l'ingresso M è attivo e lo è anche l'ingresso Ci. Il modulo ha è un semiaddizionatore (half adder) comune; gli ingressi a e b del semiaddizionatore sono intercambiabili.
|
|
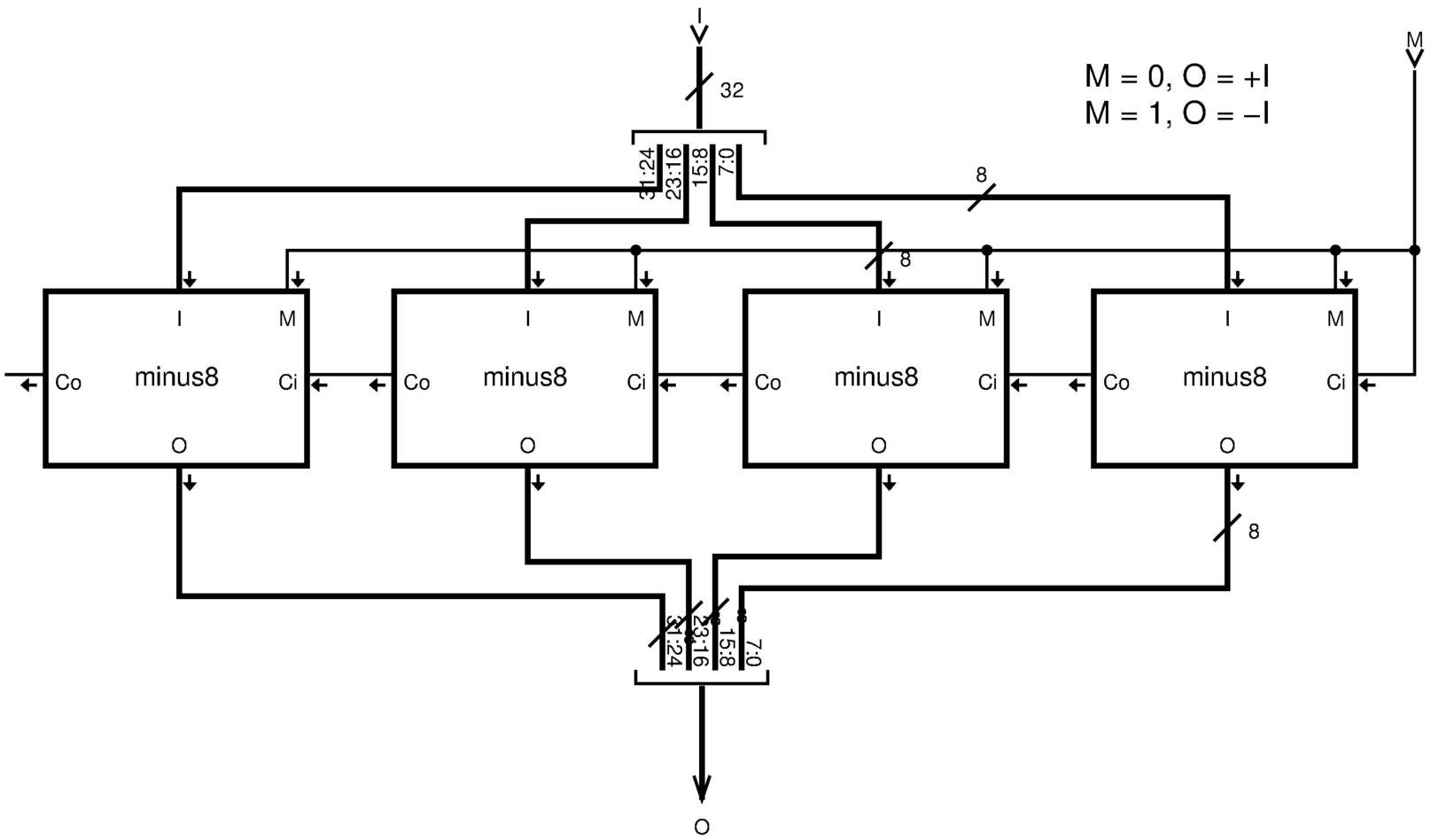
Figura u127.7. Modulo minus32: inverte il segno di un numero a 32 bit, se l'ingresso M è attivo e lo è anche l'ingresso Ci. Il modulo minus8 è descritto nella figura u127.6.
|
Somma e sottrazione
La figura successiva mostra un modulo da 8 bit per la somma e la sottrazione, gestendo opportunamente il riporto o la richiesta di prestito di una cifra e fornendo l'informazione sull'eventuale traboccamento, confrontando gli ultimi due riporti.
|
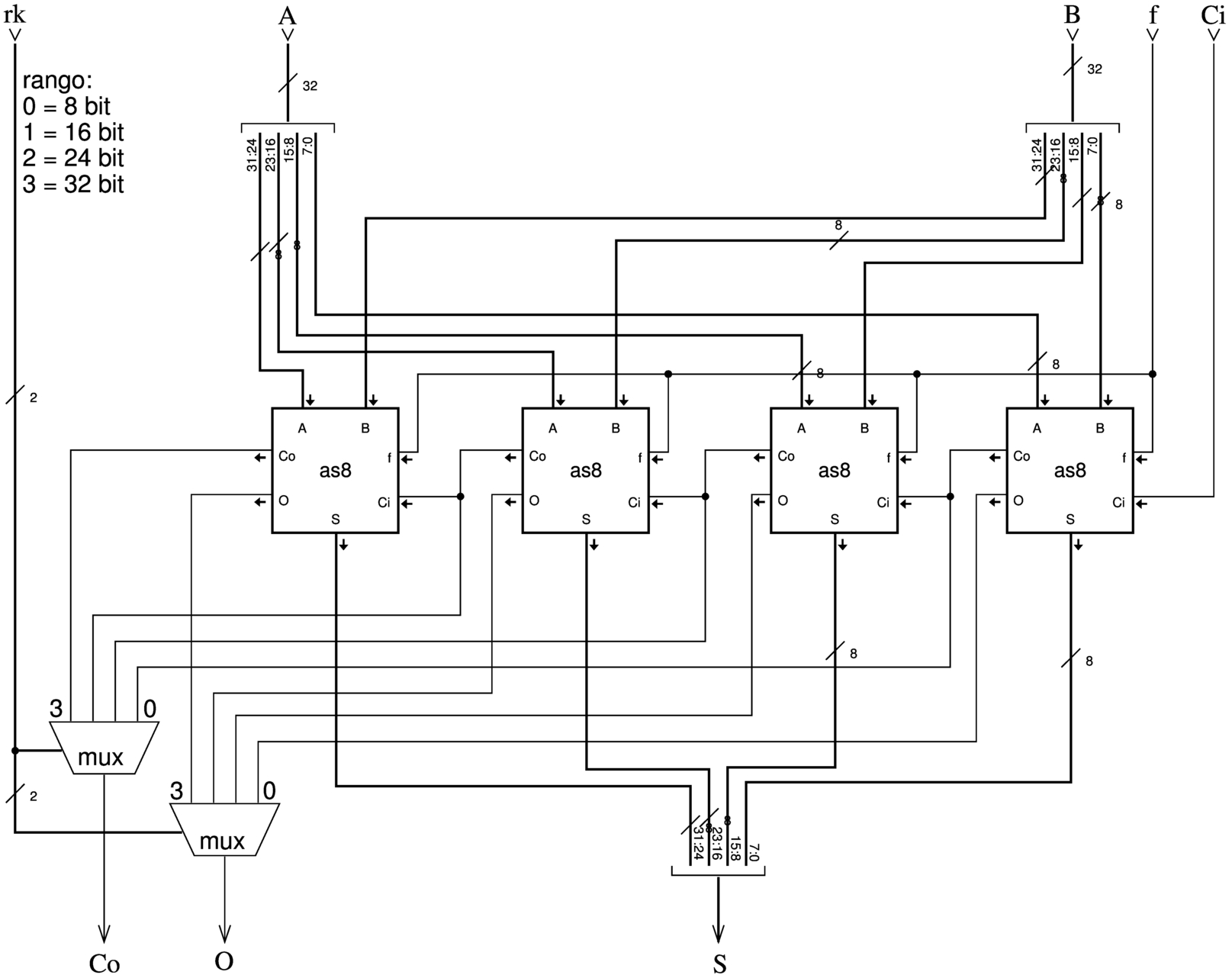
Figura u127.8. Modulo as8: somma e sottrazione di interi a otto cifre binarie. L'ingresso f (function) controlla l'applicazione di una somma o di una sottrazione; l'uscita O fornisce l'informazione sull'eventuale traboccamento. Il modulo fa è un addizionatore completo (full adder).
|
|
Figura u127.9. Modulo as32: somma e sottrazione con la possibilità di controllare il rango dei dati in ingresso e in uscita. Il modulo as8 è descritto nella figura u127.8.
|
Scorrimento e rotazione
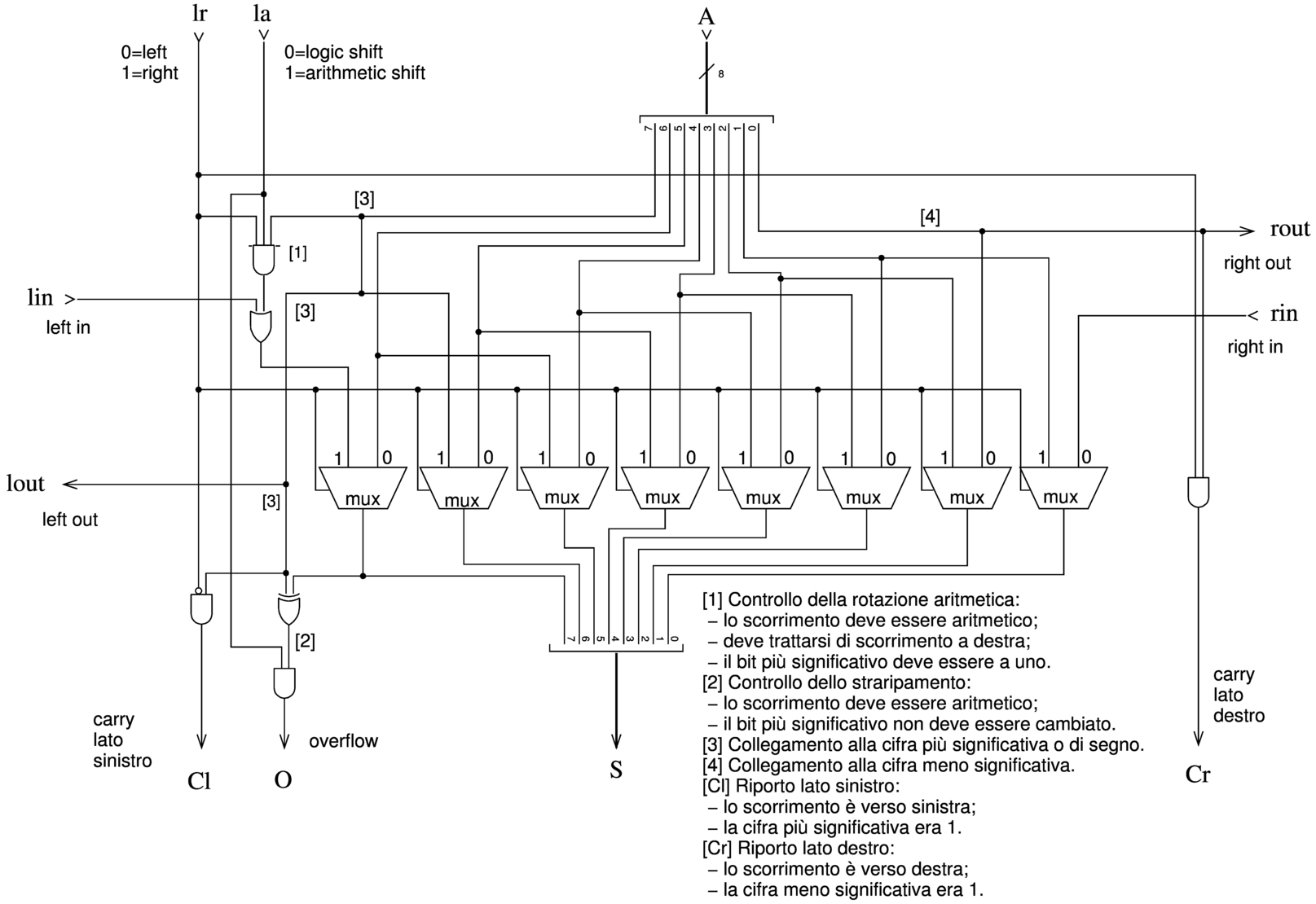
La figura successiva mostra un modulo per lo scorrimento logico e aritmetico su 8 bit. Gli ingressi e le uscite lin, lout, rin, rout (left/right in/out), servono a produrre lo scorrimento e anche la rotazione su una scala multipla di 8 bit. Le uscite Cl e Cr (carry left/right) riproducono sempre il valore del bit che viene sospinto all'esterno (dal lato sinistro o dal lato destro), mentre l'uscita O (overflow) si attiva solo in presenza di un traboccamento, dovuto a uno scorrimento aritmetico a sinistra che fa cambiare di segno al valore.
|
Figura u127.10. Modulo sh8, per lo scorrimento logico e aritmetico a 8 bit.
|
|
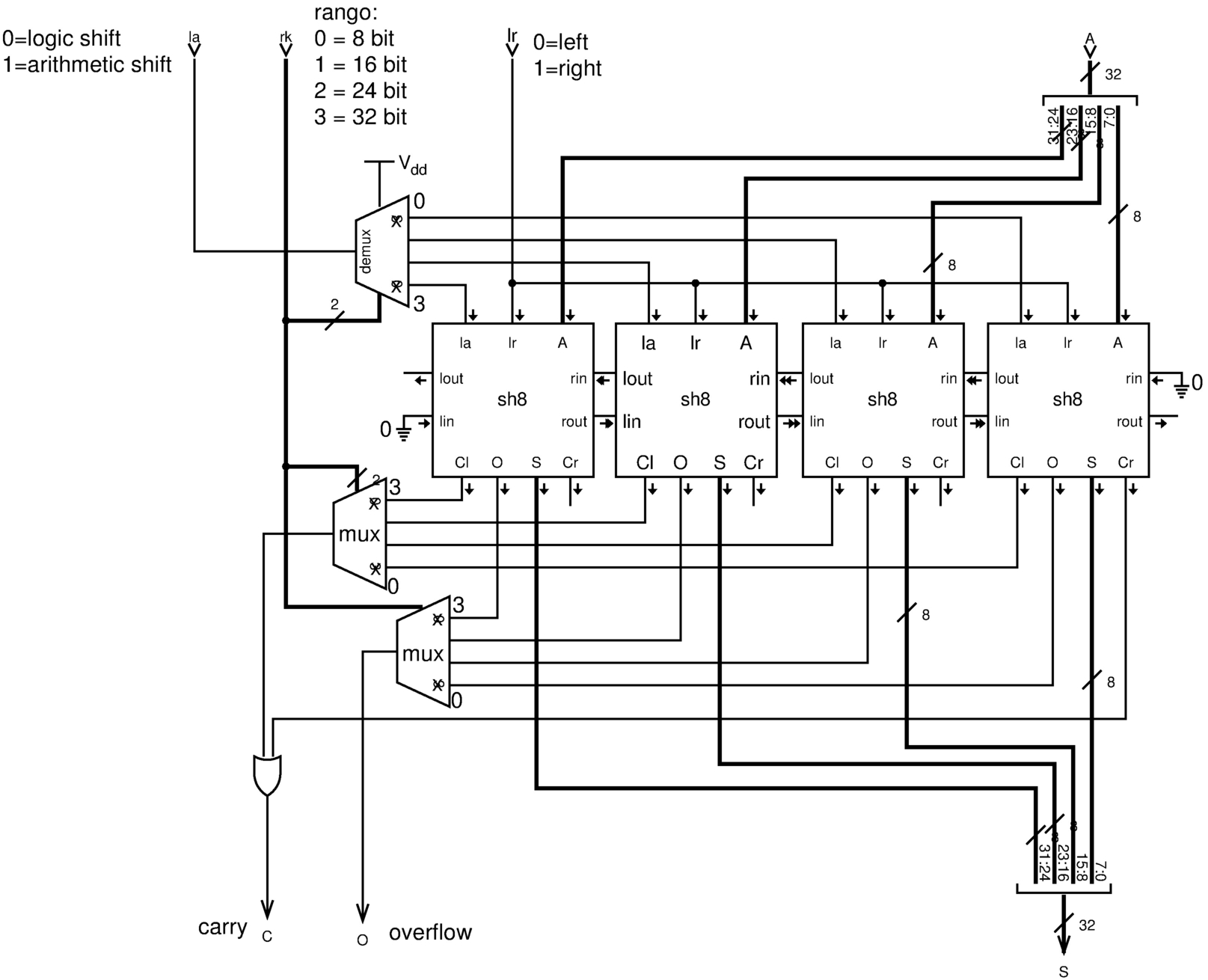
Figura u127.11. Modulo sh32: scorrimento logico e aritmetico a 32 bit, con la possibilità di intervenire su un rango inferiore. L'uscita C (carry) restituisce il valore del bit che viene sospinto a sinistra o a destra, in base al contesto. Il modulo sh8 è descritto nella figura u127.10.
|
|
Figura u127.12. Modulo ro32: rotazione a 32 bit, con la possibilità di intervenire su un rango inferiore. Dal momento che nella rotazione non si distingue tra una modalità «logica» rispetto a una aritmetica, non è presente un'uscita che possa segnalare lo straripamento. Il modulo sh8 è descritto nella figura u127.10.
|
|
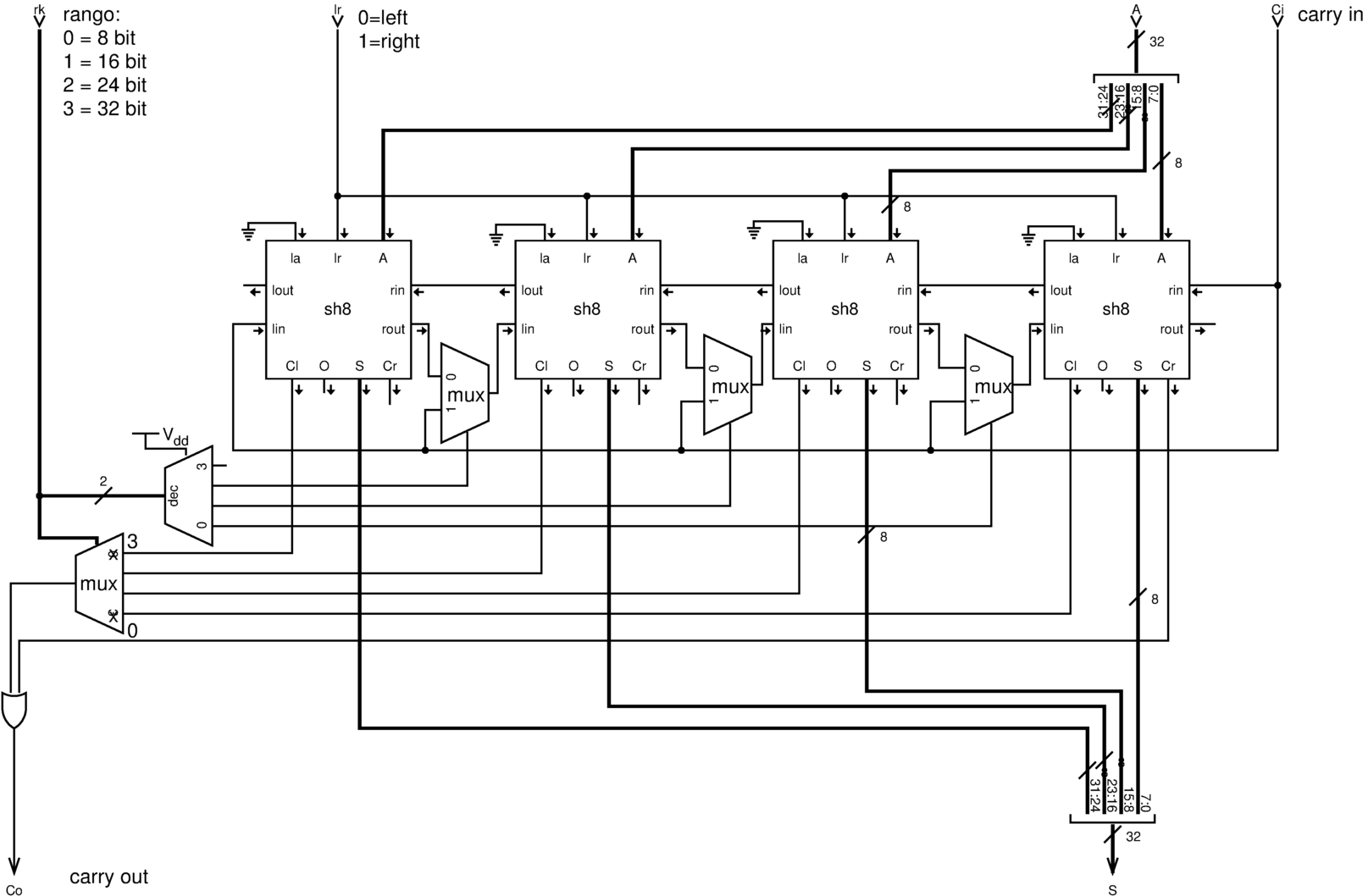
Figura u127.13. Modulo rc32: rotazione utilizzando il riporto, in quanto il valore del riporto in ingresso è ciò che viene inserito dal lato opposto alla direzione dello scorrimento. Il modulo sh8 è descritto nella figura u127.10.
|
Comparazione di valori
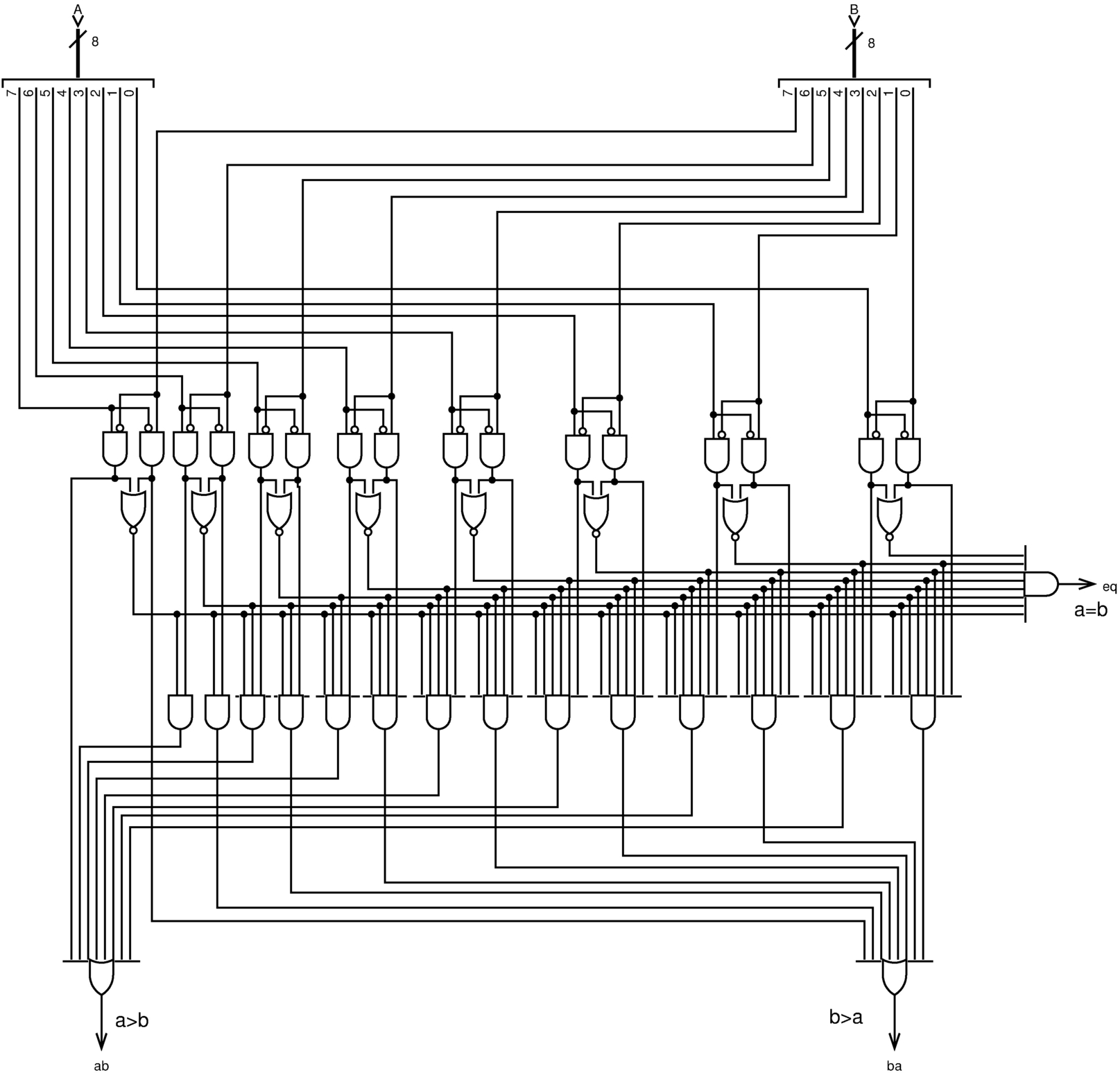
La comparazione tra due valori consente di determinare se questi sono uguali o se uno dei due sia maggiore. Il modulo cmp8 esegue una comparazione di valori senza segno, attivando un'uscita differente a seconda dei tre casi possibili: a>b, a<b, a=b.
|
Figura u127.14. Modulo cmp8: comparazione di interi, senza segno, a 8 bit.
|
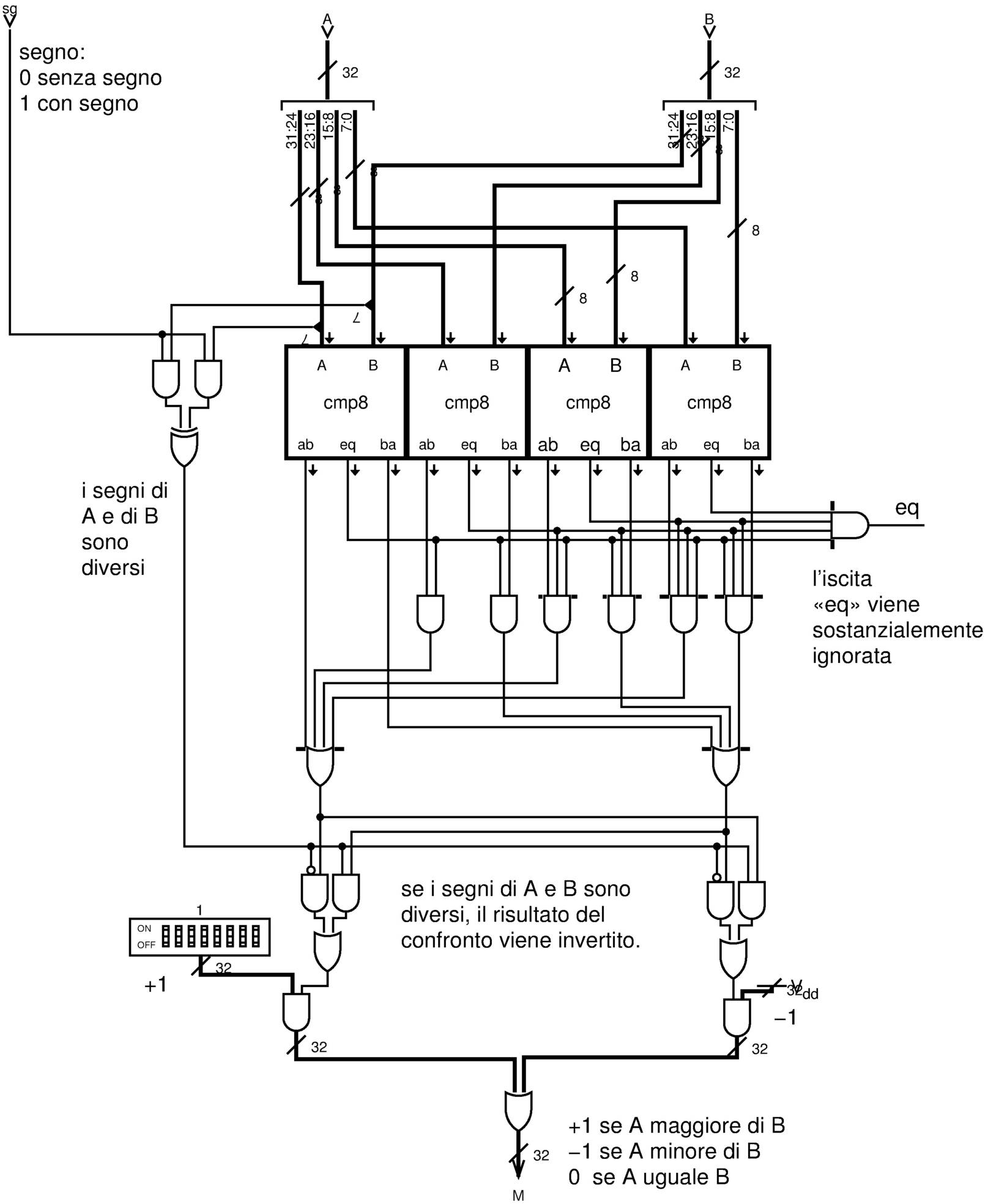
Il modulo cmp8 può essere utilizzato per il confronto di valori espressi su una quantità multipla di bit; in tal caso, si può introdurre il controllo sul segno: se i valori da confrontare si intendono con segno, se i segni dei due valori sono discordi, l'esito del confronto va invertito. Il modulo cmp32 confronta due valori a 32 bit, restituendo l'esito del confronto in forma di valore a 32 bit: zero se i valori sono uguali; +1 se A>B; -1 se A<B.
|
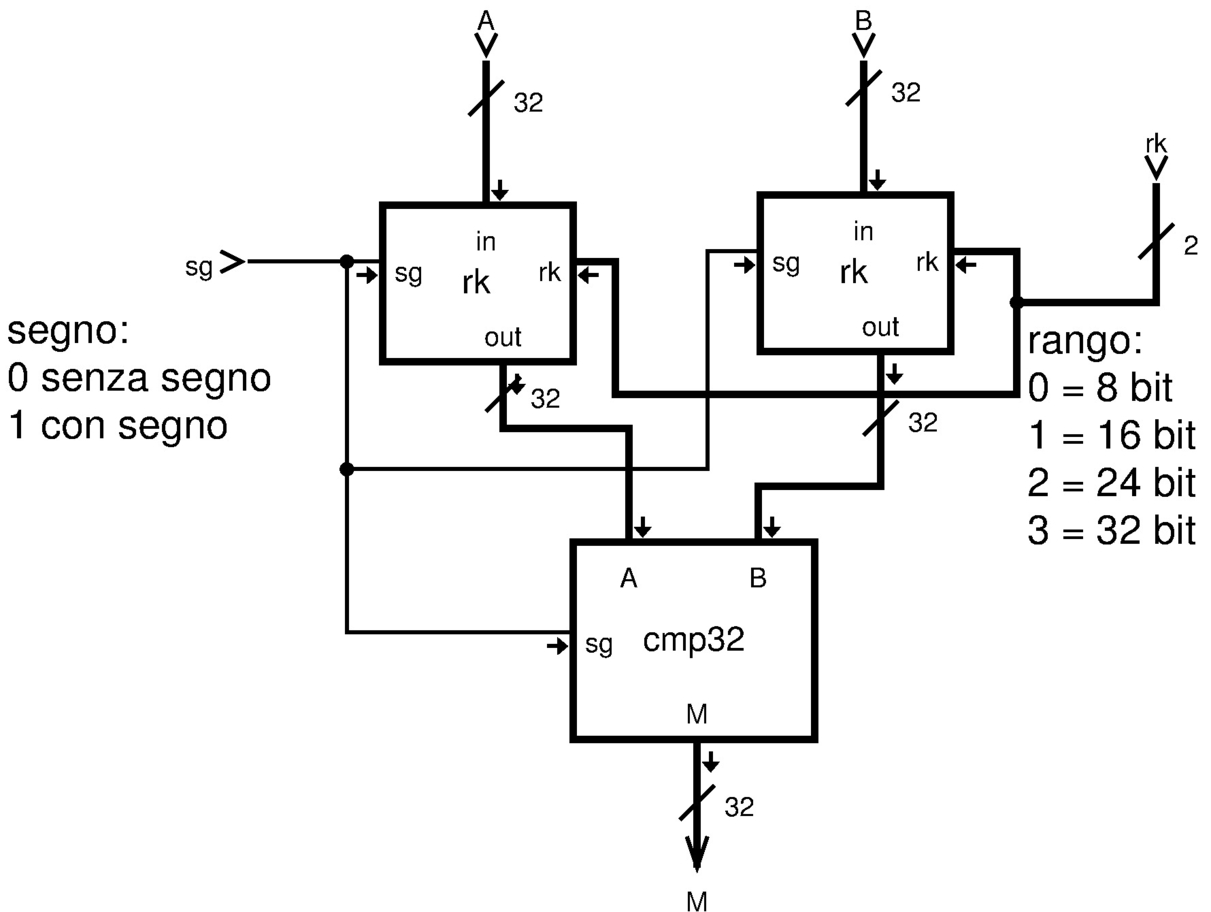
Figura u127.15. Modulo cmp32: confronto a 32 bit, con la possibilità di distinguere tra valori senza segno o con segno. Il modulo cmp8 è descritto nella figura u127.14.
|
Il modulo cmp32 non consente di ridurre il rango di bit preso in considerazione nel confronto; pertanto, se si desidera poter controllare il rango, occorre aggiungere il filtro del modulo rk (figura u127.5), come si vede nella figura successiva.
|
Figura u127.16. Esempio di filtro attraverso il modulo rk (figura u127.5).
|
Moltiplicazione
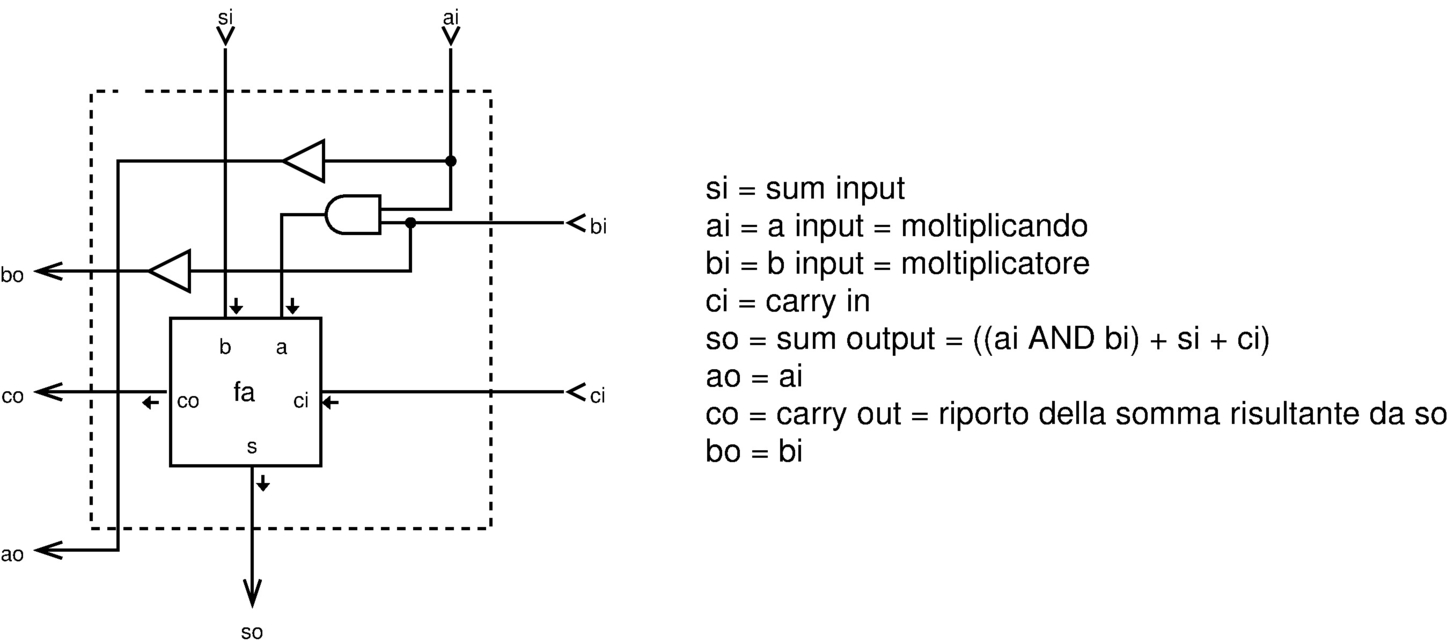
Come già descritto in precedenza, per la moltiplicazione ci si avvale di un modulo apposito che somma il risultato dell'operatore AND sui due valori in ingresso. Viene richiamato nella figura successiva.
|
Figura u127.17. Modulo mul: moltiplicazione a un bit. Questo modulo viene poi usato per la realizzazione di quello a otto bit.
|
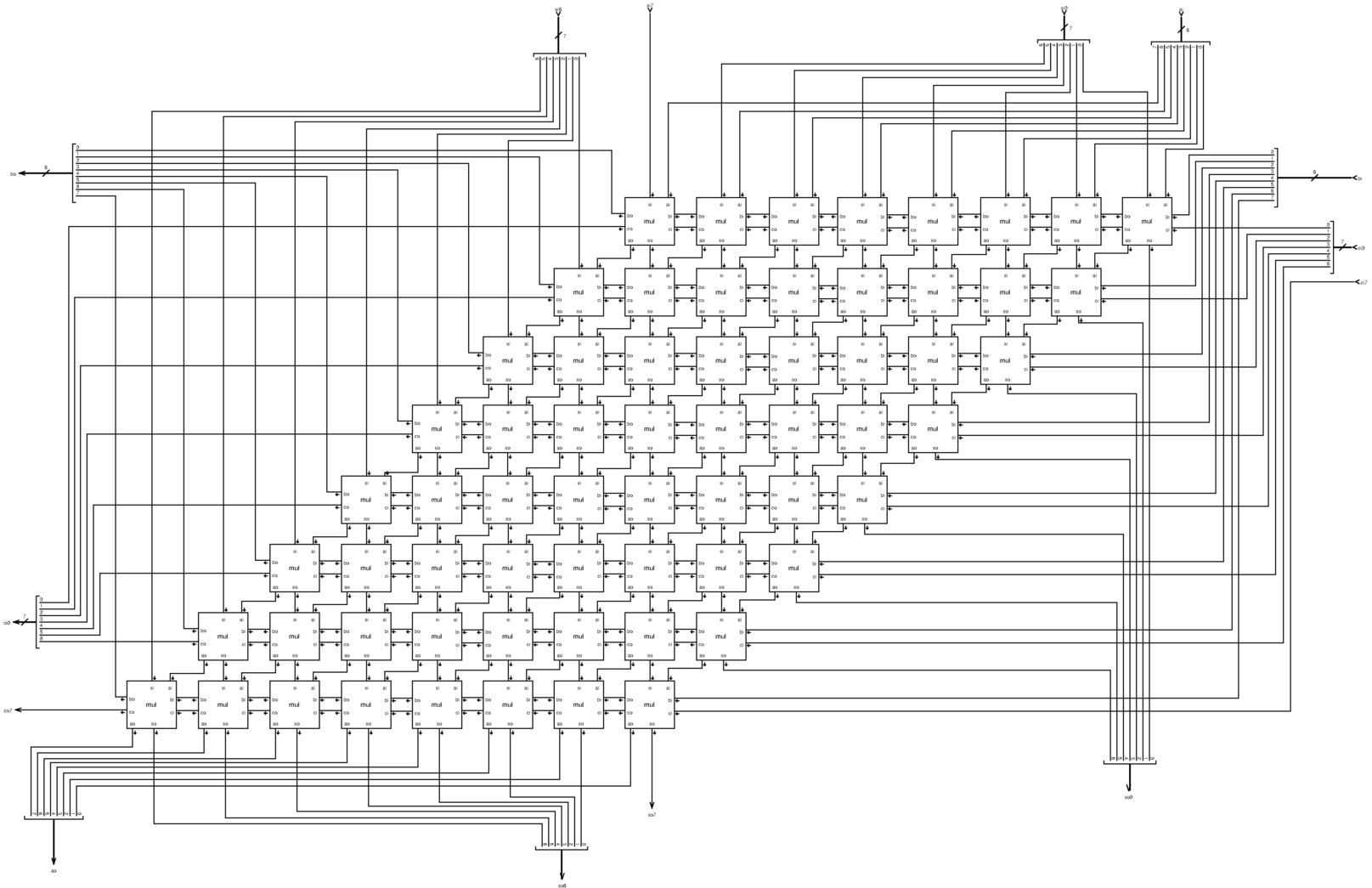
Per la moltiplicazione viene proposto il modulo mul8, a 8 bit, con tutte le connessioni necessarie a collegarlo ad altri moduli uguali, per realizzarne di più grandi in forma compatta.
|
Figura u127.18. Modulo mul8: moltiplicazione a 8 bit.
|
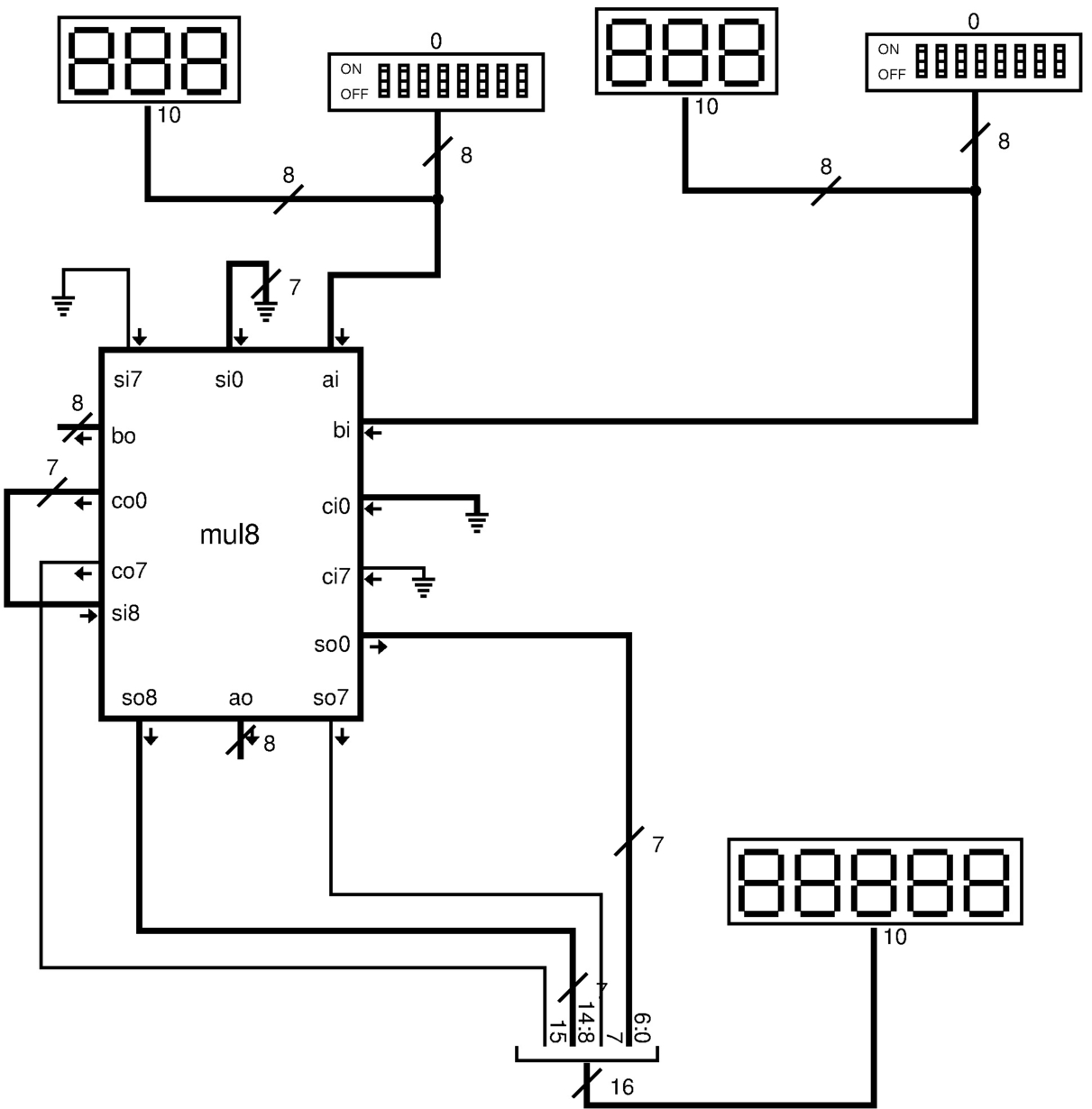
Dato che il modulo mul8 è abbastanza complesso a causa delle connessioni di cui dispone, nella figura successiva si vede come potrebbe essere utilizzato da solo, per numeri a 8 bit.
|
Figura u127.19. Utilizzo del modulo mul8 da solo.
|
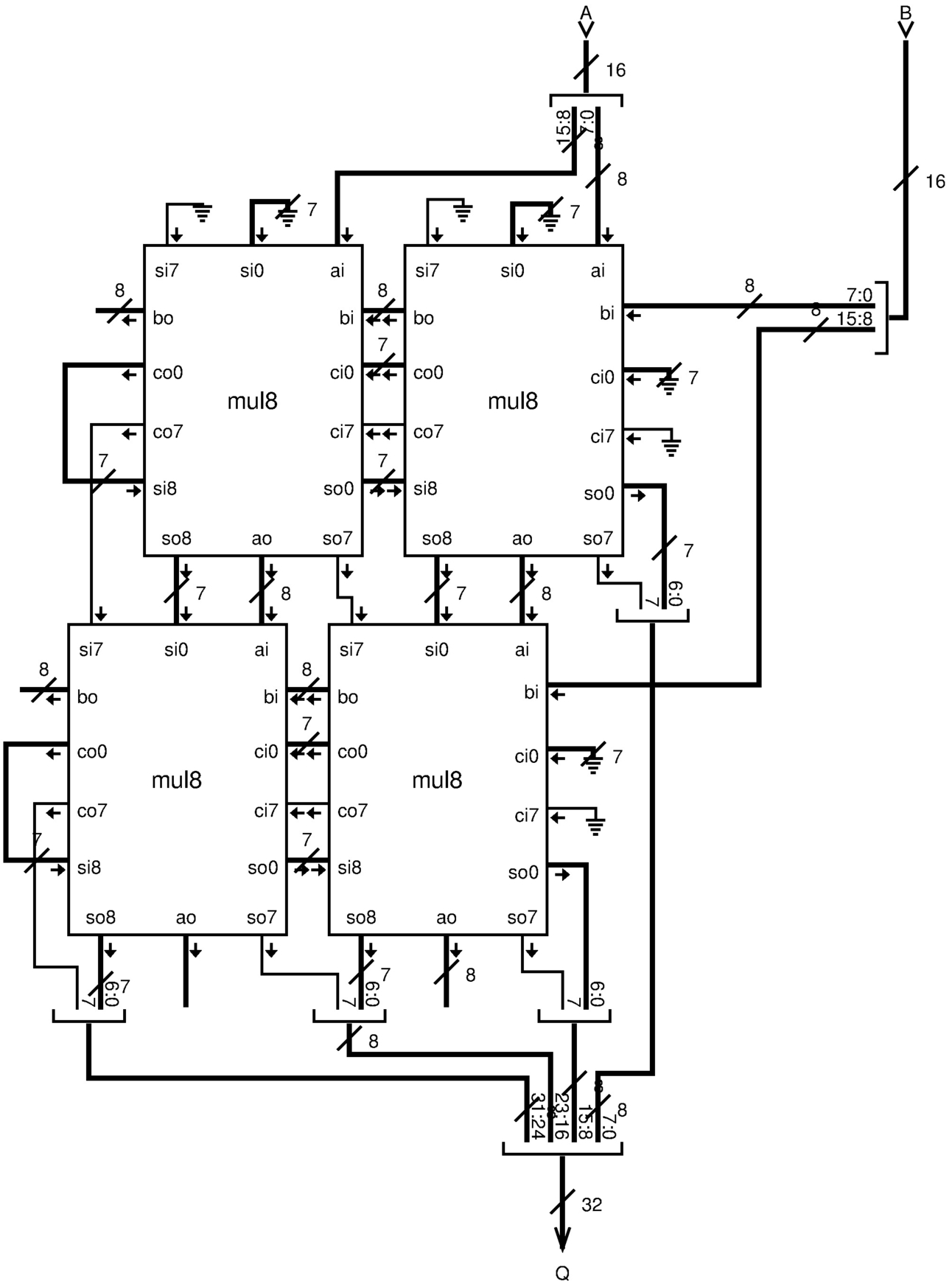
Per procedere gradualmente, si vede anche come potrebbe essere sviluppato un modulo a 16 bit, per il quale servono quattro moduli mul8.
|
Figura u127.20. Modulo mul16: moltiplicazione a 16 bit senza segno. Il modulo mul8 è descritto nella figura u127.18.
|
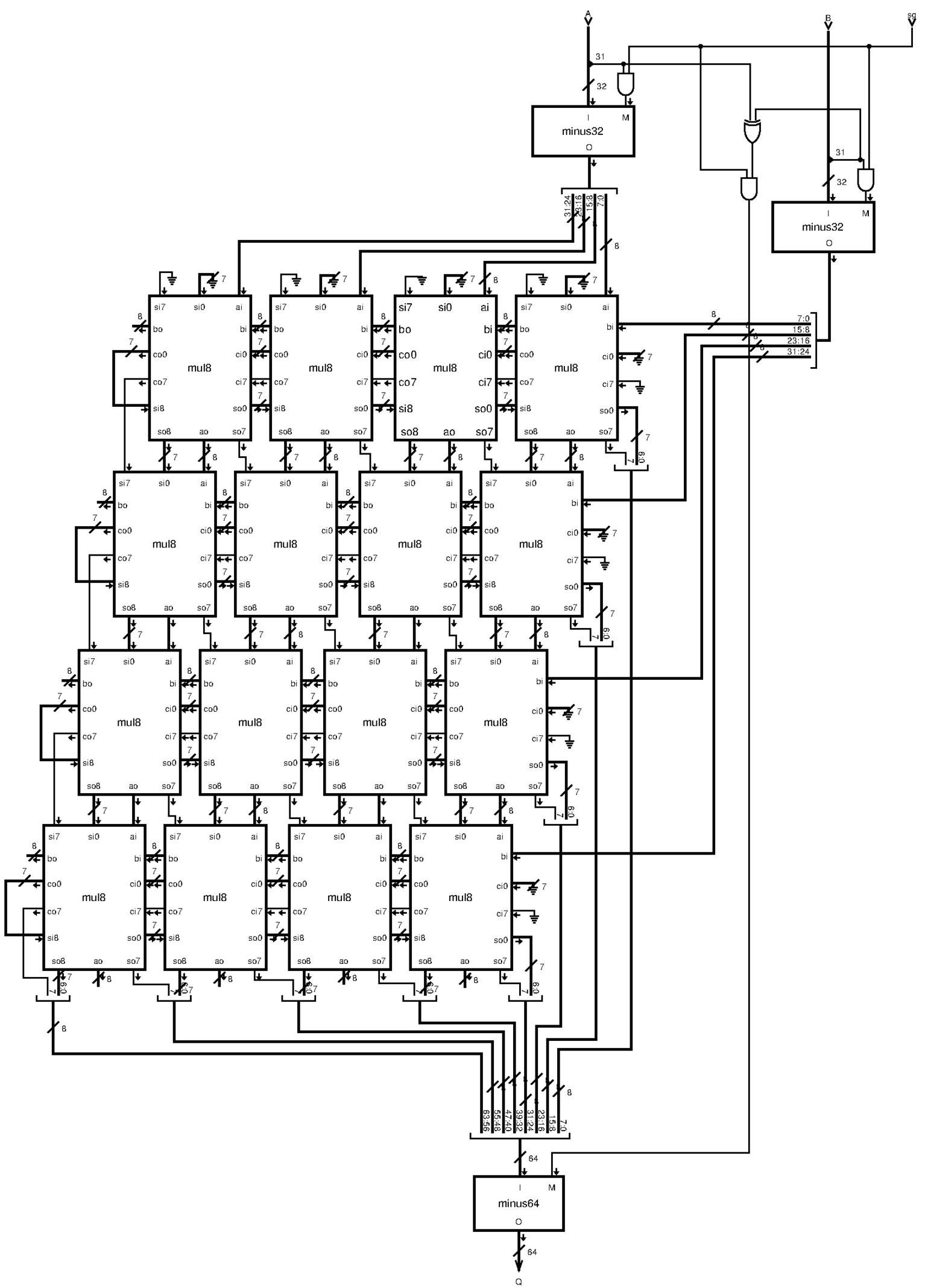
|
Figura u127.21. Modulo mul32: moltiplicazione a 32 bit con segno. Il modulo mul8 è descritto nella figura u127.18, mentre i moduli minus... sono descritti a partire dalla figura u127.6.
|
Divisione
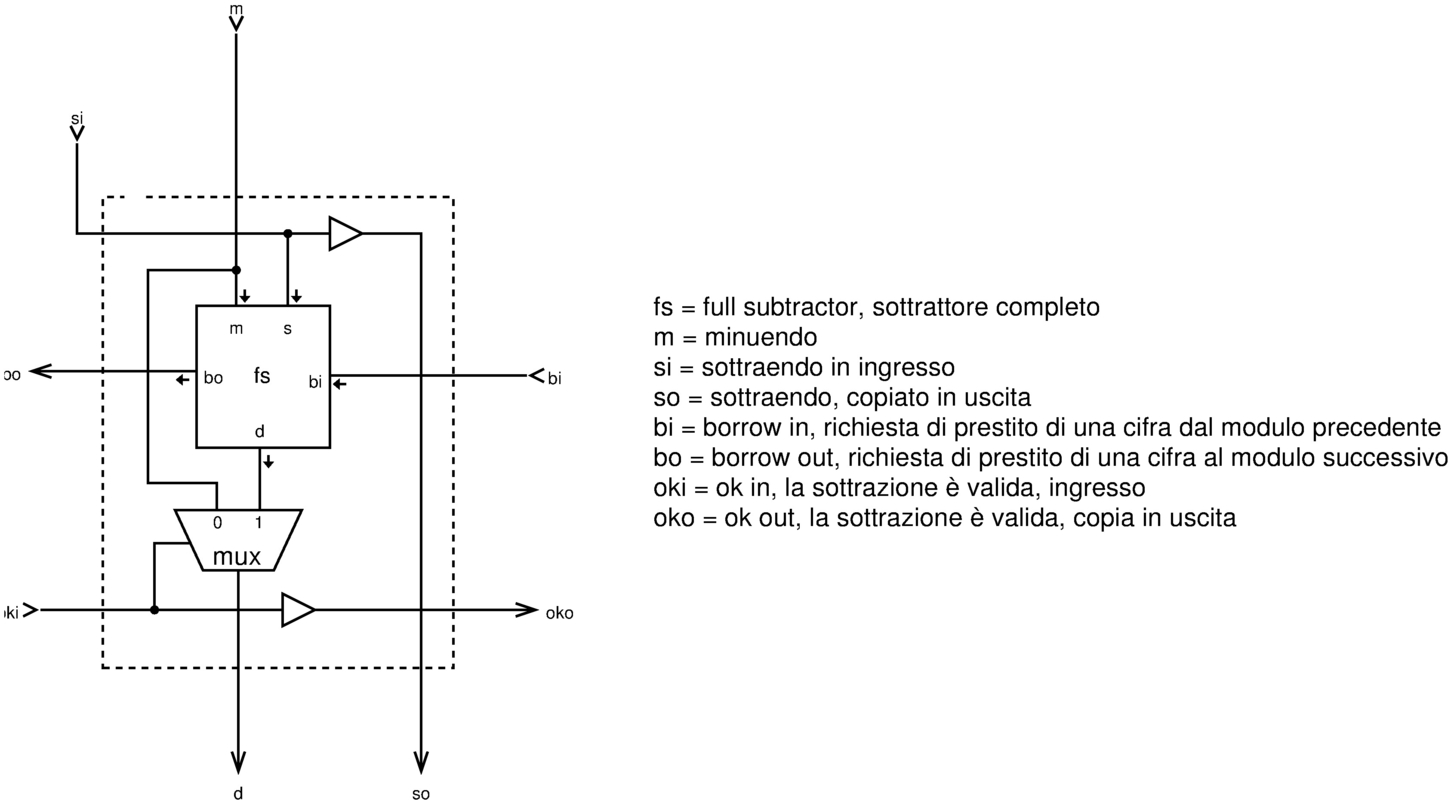
Per la divisione ci si avvale di un modulo che esegue la sottrazione del divisore dal dividendo, in fasi successive. Il modulo in questione è già apparso in precedenza nel capitolo, ma viene ripresentato per maggiore comodità.
|
Figura u127.22. Modulo div: componente usato per il calcolo della divisione, attraverso la sottrazione del divisore dal sottraendo. Questo modulo consente di operare su un solo bit. Ci si avvale del modulo fs, corrispondente a un sottrattore completo (full subtractor), descritto nella sezione u0.10.
|
|
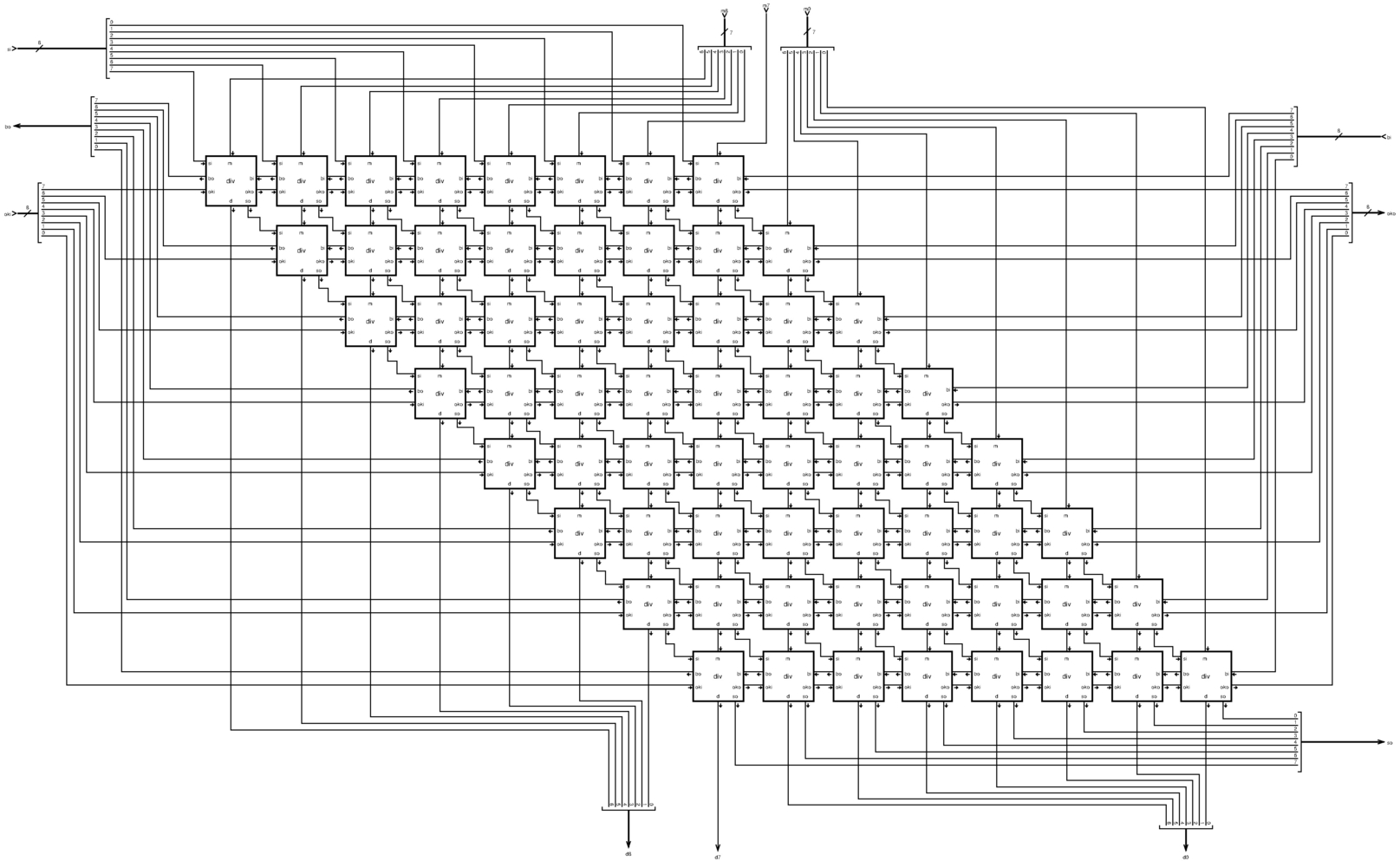
Figura u127.23. Modulo div8: divisione intera a 8 bit, senza segno. Si utilizzano 64 moduli div per sottrarre dal dividendo il divisore, fino a trovare il quoziente e il resto. Il modulo è organizzato in modo da potersi connettere con altri moduli uguali e operare su interi aventi un numero maggiore di cifre. Il modulo div è descritto nella figura u127.22.
|
|
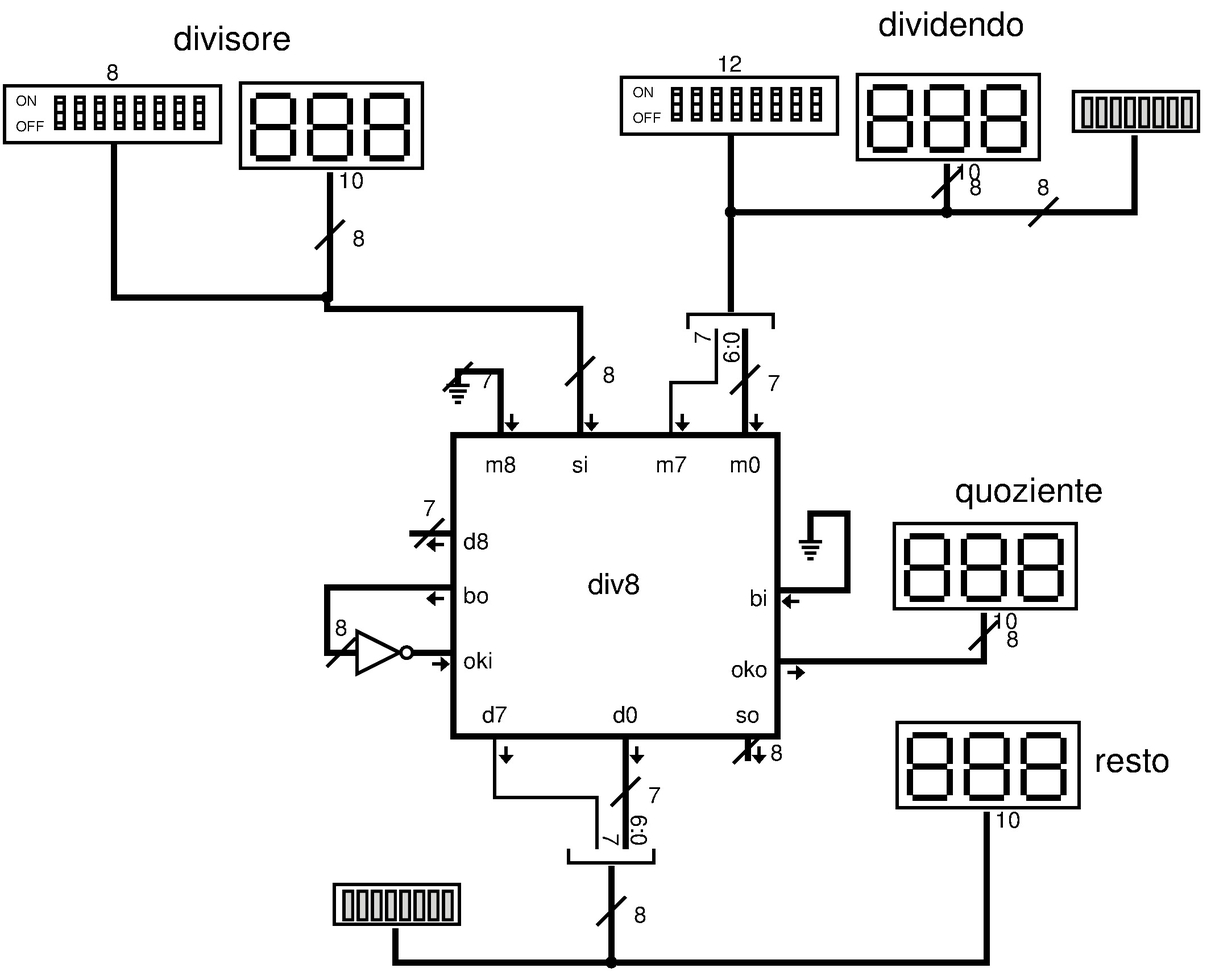
Figura u127.24. Esempio di utilizzo del modulo div8, per dimostrare in che modo vanno usati i collegamenti di cui è provvisto. Il modulo div8 è descritto nella figura u127.23.
|
|
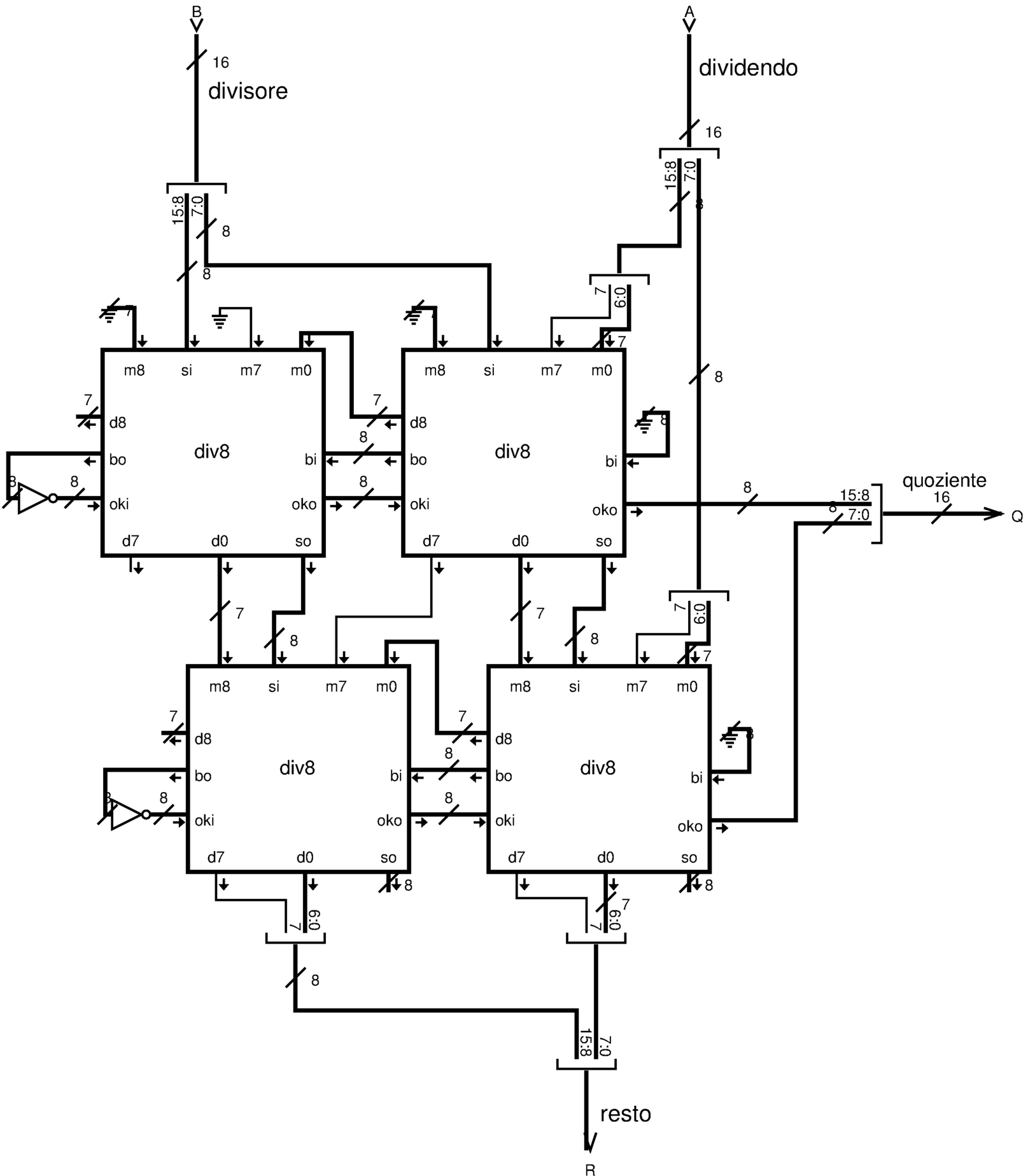
Figura u127.25. Modulo div16: divisione intera, senza segno, a 16 bit. Si utilizzano quattro moduli div8 collegati opportunamente tra loro. Il modulo div8 è descritto nella figura u127.23.
|
|
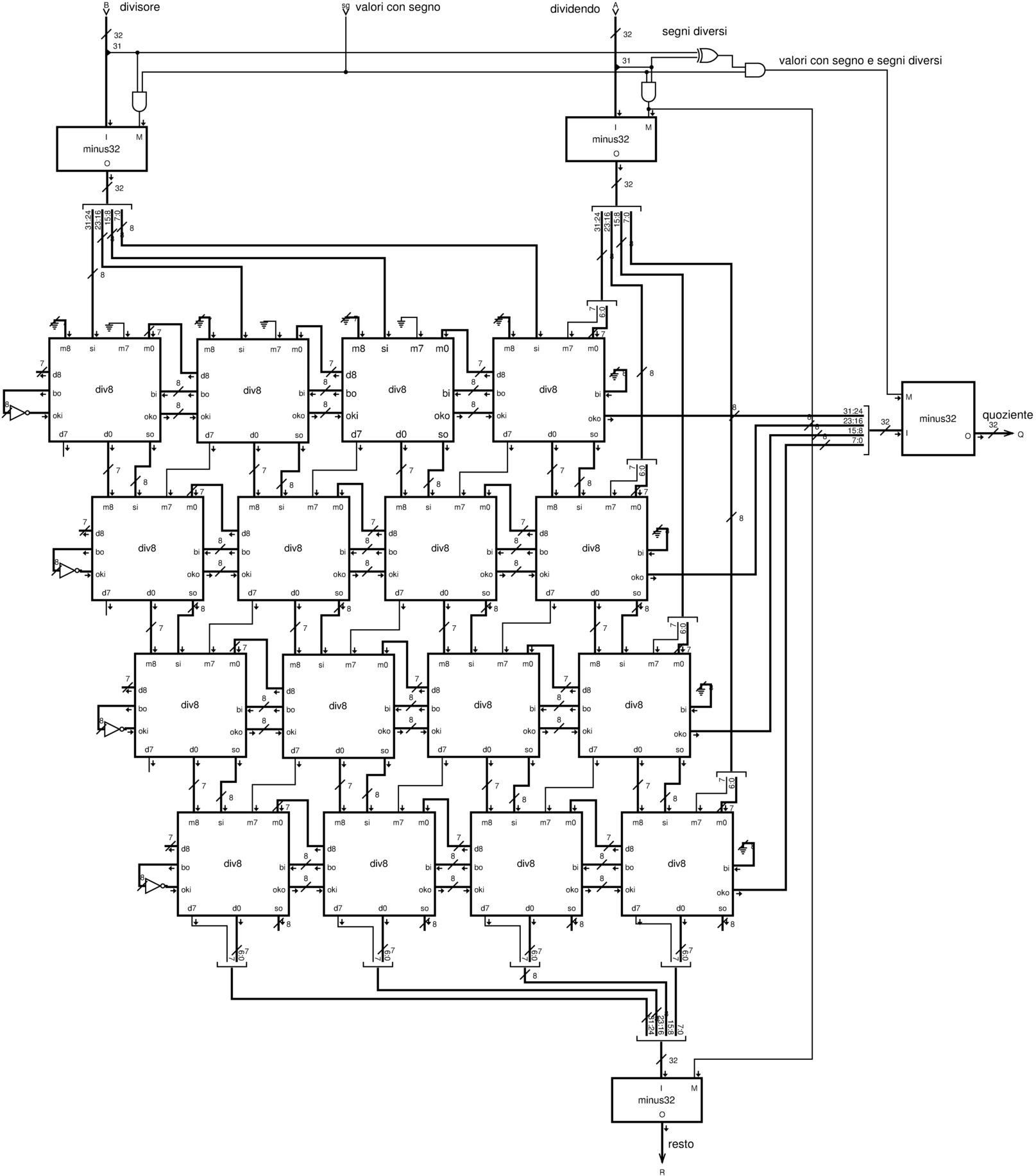
Figura u127.26. Modulo div32: divisione intera, con o senza segno, a 32 bit. Si utilizzano sedici moduli div8 e quattro moduli minus32 per il controllo del segno, se è richiesto un calcolo che ne tenga conto. Il modulo div8 è descritto nella figura u127.23, mentre il modulo minus32 è descritto nella figura u127.7.
|
Unità logica
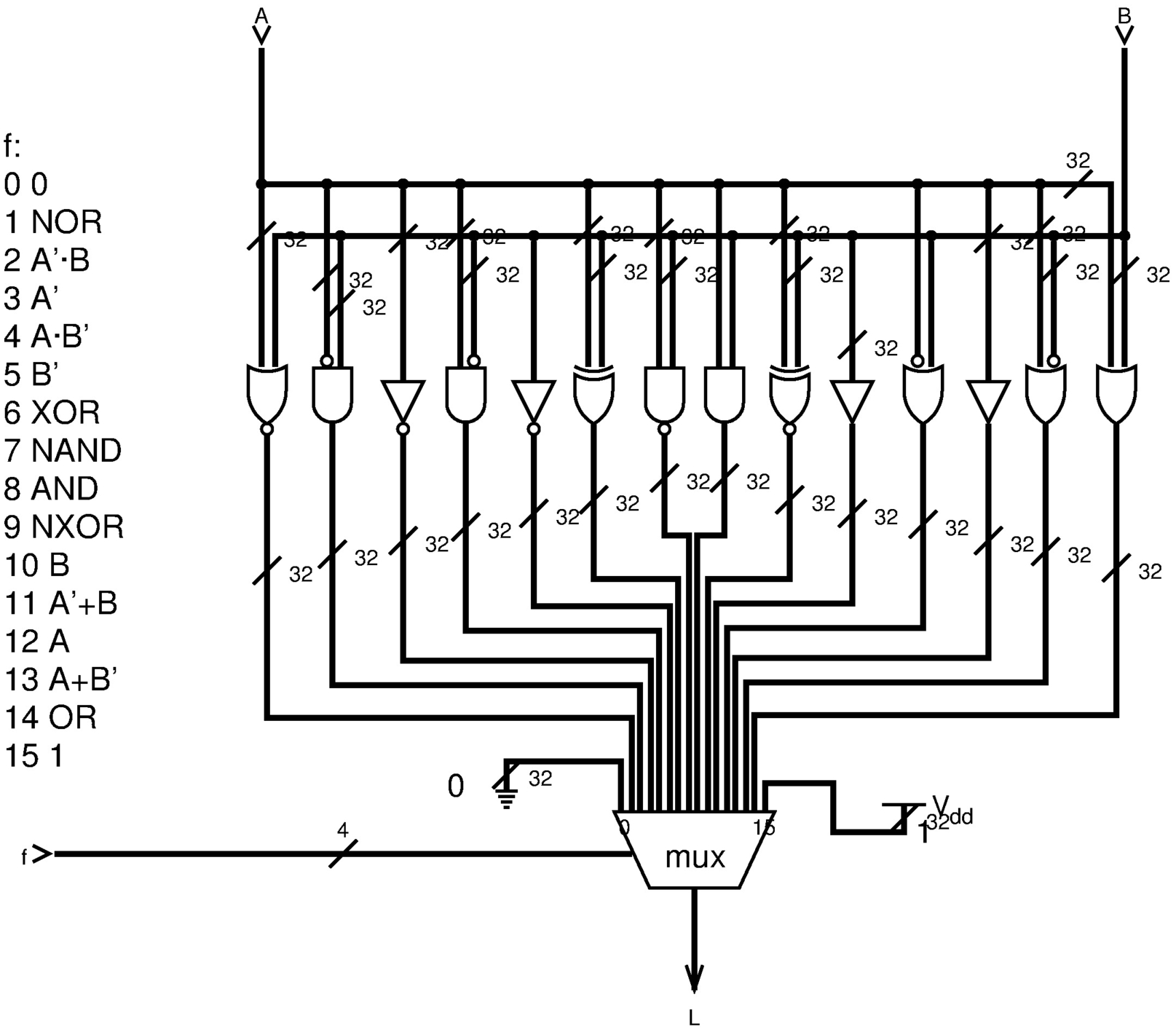
Per unità logica si intende quella che esegue operazioni booleane, bit per bit, su valori interi espressi in forma binaria. Di solito le operazioni disponibili sono poche (AND, OR, NOT, XOR), ma nell'esempio della figura successiva appaiono tutti i casi già descritti nella tabella u126.4, anche se ciò può essere superfluo.
|
Figura u127.27. Modulo logic32: realizza le 16 operazioni logiche che si possono ottenere da un circuito combinatorio con due ingressi e un'uscita. In questo caso, ogni componente ne rappresenta in realtà 32, in parallelo: solo l'ingresso f che serve a selezionare la funzione, è sempre lo stesso.
|
ALU completa
Nella figura successiva viene proposta una, ALU completa di tutti i moduli descritti in questo gruppo di sezioni. Valgono le osservazioni seguenti:
-
i moduli della rotazione sono gestiti come se fossero uno solo, in cui la funzione di rotazione con o senza riporto avviene in base alla selezione del tipo di scorrimento; inoltre, sia per lo scorrimento, sia per la rotazione, è possibile scegliere su quale ingresso intervenire;
-
per risolvere in qualche modo il problema del risultato della moltiplicazione, che occupa 64 bit, si è scelto di selezionare quale porzione del risultato si vuole ottenere, anche se ciò comporta in pratica un raddoppio del tempo necessario alla moltiplicazione, perché ogni volta il calcolo viene ripetuto;
-
i moduli pescano dalla linea dell'ingresso F (function) i bit che gli servono per adeguare il proprio comportamento, tenendo conto che i primi quattro bit di F servono ai multiplatori che selezionano le uscite da prelevare, mentre i quattro bit più significativi sono quelli che sono affidati ai moduli rispettivi.
Si comprende che si tratta di una soluzione che non è ottimale dal punto di vista delle prestazioni, avendo soltanto uno scopo dimostrativo.
|
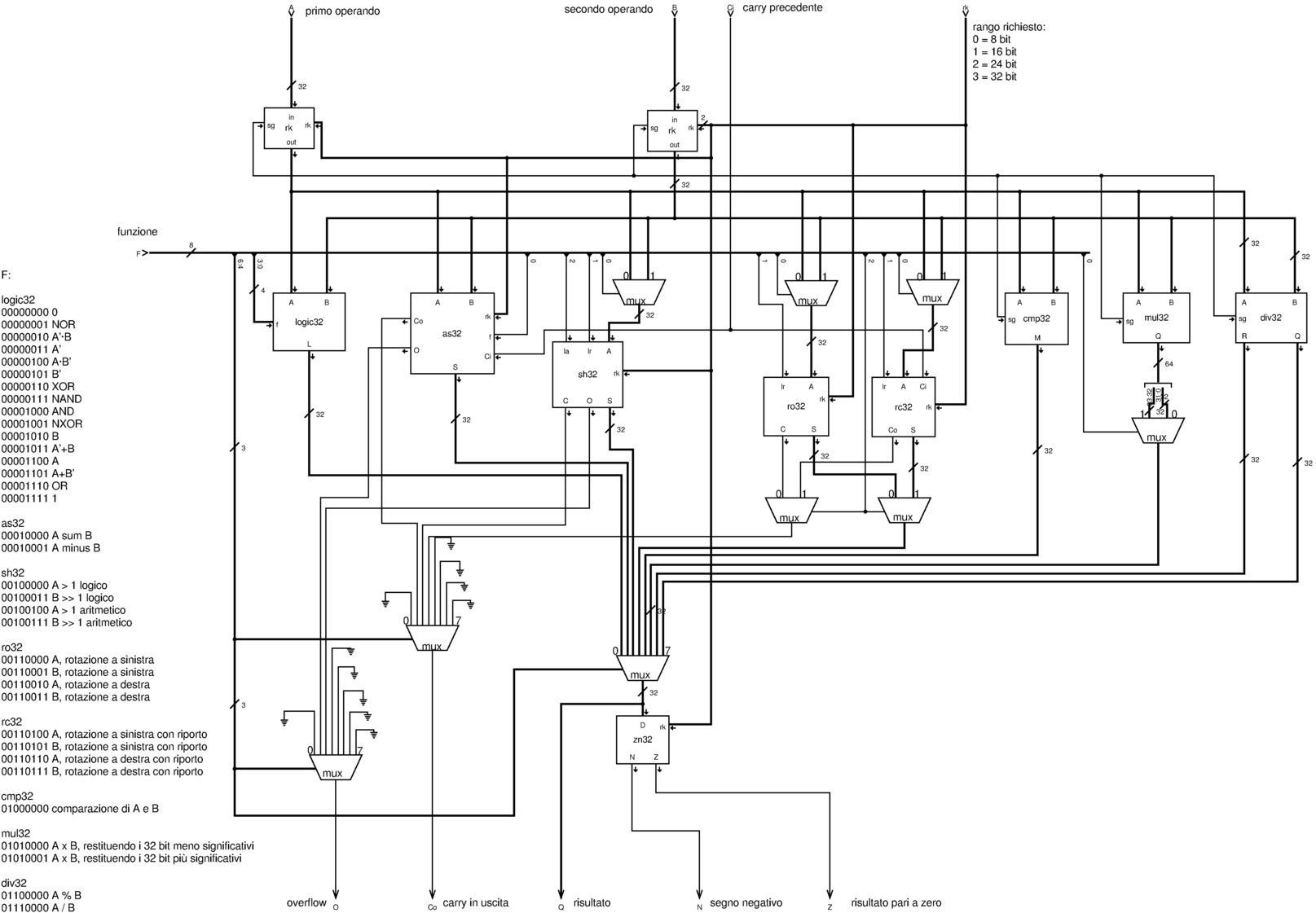
Figura u127.28. Modulo alu32: ALU completa a 32 bit. L'ingresso F determina il comportamento della ALU.
|
«a2» 2013.11.11 --- Copyright © Daniele Giacomini -- appunti2@gmail.com http://informaticalibera.net